

土地家屋調査士試験では複素数を使ったほうが計算が簡単って聞いたんだけど・・・
そもそも複素数ってなに?分かりやすく説明してほしい!
そんな疑問にお答えします。
土地家屋調査士試験について調べていると「複素数」というキーワードを必ず見かけます。
複素数を使えば計算が楽になるわけですが、具体的にどのように使いこなせばいいのか分からない人も多いはずです。
予備校に通っている人なら授業の中で学習するはずですが、問題は独学の場合ですよね。
私自身は半年の独学で一発合格をしているわけですが、関数電卓の基礎から実践まで、100%自力で学習しました。
使用していたメインの関数電卓はキャノン「F-789SG-SL」です。
交点計算用のサブの関数電卓はカシオ「fx-375ES-N」でした。
参考:【土地家屋調査士】一発合格した私がオススメする関数電卓3選!《試験対応》
今回はキャノン「F-789SG-SL」を使った計算方法をまとめていきます。それぞれの項目でより詳しく解説している記事を貼っているので理解を深めたい人は飛んでください。
この記事で分かること
- 複素数の定義なんて知らなくてもいい理由
- 関数電卓 キャノン「F-789SG-SL」を使った計算方法
こちらの記事は動画で見ることができます。
複素数とは何か?

複素数=虚数「i」
そもそも複素数って何?と思う人も多いですよね。
複素数とは虚数「i」のことです。さっそく意味不明な言葉が出てきましたが安心してください。
ぶっちゃけ、複素数の厳密な定義なんて知らなくても大丈夫です。
「関数電卓の機能である複素数モードを使えば計算が簡単になる」という認識でOKです。
どうしても詳細を知りたいという人は高校数学の授業で出てくるのでググってみてください。
というわけで、関数電卓で複素数を使う方法について解説していきます。
土地家屋調査士試験で使う複素数を利用した計算法(F-789SG-SL)

冒頭でも言ったとおり、私はメインの計算をF-789SG-SL(キャノン)、交点計算をfx-375ES-N(カシオ)でやっていました。
- F-789SG-SL(キャノン)・・・二点間距離、方向角、座標、面積
- 交点計算をfx-375ES-N(カシオ)・・・交点計算
こんな感じです。
個人的にはこの使い分けが一番だと思っています。てことでこれらの計算方法を解説していきます。
※今回はキャノンの関数電卓で交点計算をします。カシオの場合はリンク先を参照。
複素数を使う前の設定方法
初期設定では複素数は使えません。てことでまずは基本的な設定をしていきます。
- 設定のリセット
- 分数表示からライン表示に変更する
- 小数点以下の表示範囲の設定
- 複素数モードに変更
最初にやることはこんな感じですね。
こちらに詳しく解説しています。打ち方も画像付きで書いているので参考にしてください。
参考:【土地家屋調査士】関数電卓[F-789SG]の使い方|設定をリセット、メモリー方法、ライン表示、丸め、複素数モードに変更

座標入力・メモリーの方法
| X | Y | |
| T1 | 100 | 100 |
| T2 | -150 | 200 |
土地家屋調査士試験の土地の問題では座標を使った計算をします。
上に貼っている表みたいなものがほぼ100%問題文にあります。
問題文には既知点(すでに分かっている点)の座標値が載っているのでそれらを関数電卓に記録していくわけです。
打ち方はこんな感じ。
※T2も同じようにBに入れてください。
こちらで詳しく解説しています。
参考:【土地家屋調査士】関数電卓[F-789SG]の使い方|座標入力・メモリーの方法(複素数)

二点間距離の計算方法

では、先ほど入力したT1とT2の距離を求めてみます。
答えはフル桁だと269.2582404です。
注意点ですが、「辺長を答えなさい」という問題では、解答欄には小数点以下第3位を四捨五入した数値を記入します。
この場合の答えは「269.26m」ってことです。
こちらで詳しく解説しています。
参考:【土地家屋調査士】関数電卓[F-789SG]の使い方|二点間距離の求め方(複素数)

方向角の計算方法
続いては方向角です。方向角って何?という人のために簡単に解説しておきます。
出典:国土地理院
- 磁北…方位磁石が指す「北」のこと。この北を基準にして右回りに測った角度を磁方位角という。
- 真北…北極点、つまり地球の自転軸の北端(北緯90度地点)を指す方位。つまり普通の「北」のこと。この北を基準にして右回りに測った角度を方位角という。
- 座標の北(方眼北)…平面直角座標のX軸(縦軸)を0度(北)として右回りに測った角度のこと。この北を基準にして右回りに測った角度を方向角という。
ちょっと難しいですが、図を見ながら理解すれば分かりやすいと思います。
土地家屋調査士試験で使うのはほとんどが方向角です。たまに引っ掛け問題で方位角がでますね。
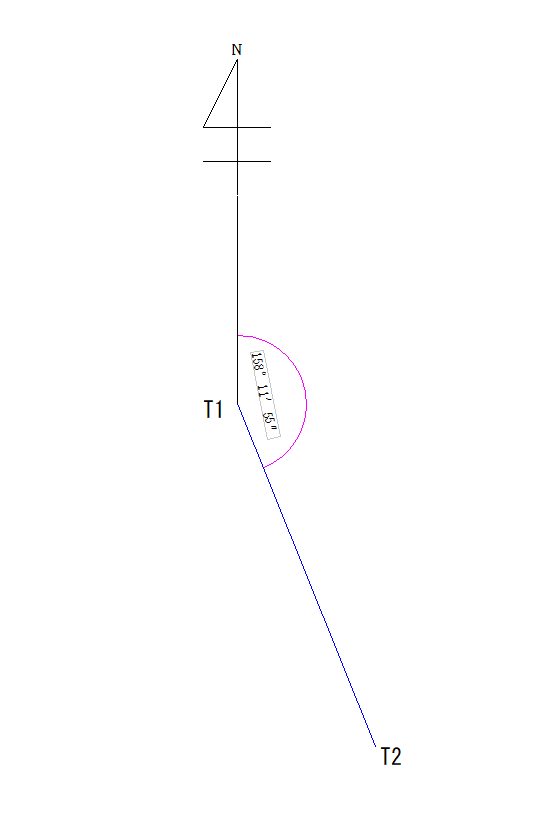
T1からT2の方向角の求め方
方向角は小数点以下の表示範囲は丸めてもいいし、フル桁でもいいです。
一応、小数点以下第2位までの表示にしておきます。
では、ピンクの角度を求めます。打ち方はこんな感じ。
答えは158.20(フル桁なら158.1985905)となり、[°′″]を押すと158°11′54.93″となります。
この答えを解答欄に書くなら158°11′55″になります。(秒以下を四捨五入した)
参考:【土地家屋調査士】関数電卓[F-789SG]の使い方|方向角の求め方(複素数)

座標の計算方法
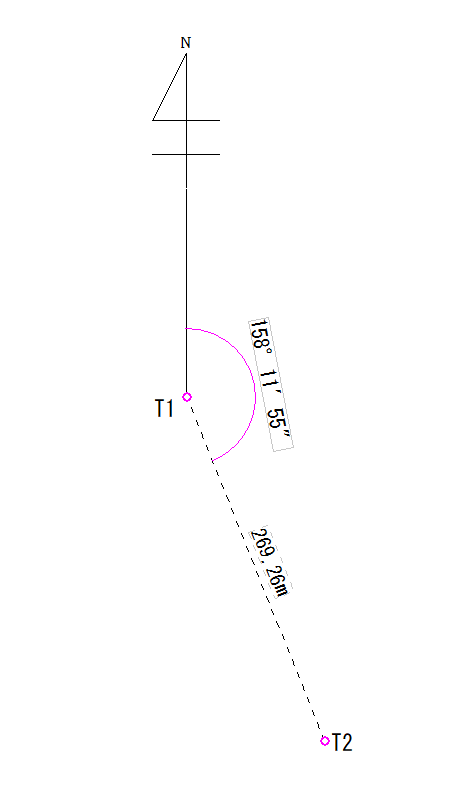
今回はT1の座標値、T1からT2までの距離と方向角が分かっている場合にT2の座標値を計算で出す方法です。
位置関係はこのような状態です。既知点T1があり、座標が不明なT2があります。
- 既知点T1(X座標…100, Y座標…100)
- T1からT2までの距離…269.26m
- T1からT2までの方向角…158°11′55″
公式はこんな感じ。
既知点の座標値+未知点までの距離∠未知点までの方向角
では、電卓に打ち込んでみます。
答えは(-150,200)ですね。
| X | Y | |
| T1 | 100 | 100 |
| T2 | -150 | 200 |
最初に座標入力したT2と同じ数値です。

座標の計算結果は丸める(四捨五入)
さて、ここで注意点です。
関数電卓を使って座標を計算した場合、表示上では(-150,200)になっていますが、フル桁にすれば端数が残っています。
先ほどの計算結果のままフル桁に戻してみます。
実際にフル桁に戻すとX座標は-150.0016697、Y座標は200.0005636になりますよね。
最初に小数点以下の表示範囲の設定をしましたが、これは画面上の表示を変更するだけってことです。
『座標値は計算結果の小数点以下第3位を四捨五入し、小数点以下第2位までとする』という公式の指示があるので、端数を四捨五入した値をメモリーをして記録しないと後々の計算がずれていきます。
今、小数点以下第3位を四捨五入し、小数点以下第2位までの表示になっていますが、この表示通りの座標値(X=-150.00、Y=200.00)を電卓に記憶させます。
これを「座標を丸める」といいます。やり方はこちら。
※必ず、丸めてから座標をメモリーしてください。
「意味が分からない!」という人が多いと思いますが安心してください。
詳しくはこちらで解説しています。画像付きなので分かりやすいと思います。
参考:【土地家屋調査士】関数電卓[F-789SG]の使い方|座標計算と丸め(四捨五入)《複素数》

面積の計算方法
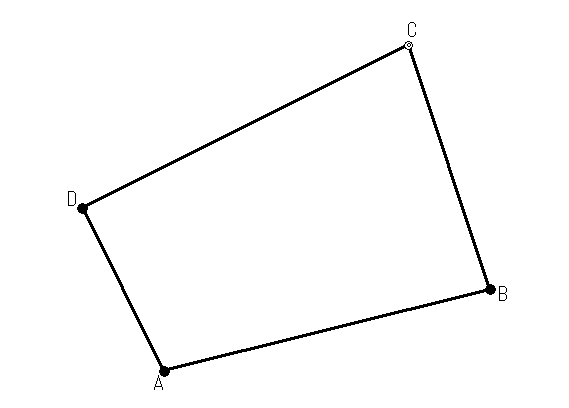
| A | 100 | 100 |
| B | 150 | 300 |
| C | 300 | 250 |
| D | 200 | 50 |
今度は面積の求め方です。まずはA~Dまで関数電卓にメモリーします。
それから、面積計算はフル桁で行います。
では、面積を求めていきます。
基本のパターン
この公式はかなり複雑なので入力ミスがないように気を付けてください。
AConjg(B)+BConjg(C)+CConjg(D)+DConjg(A)=倍面積
倍面積というのは実際の面積の倍(×2)の数字のことです。
打ち方はこんな感じ。

この数字が出ますね。そのまま[÷] [2] [=]してください。
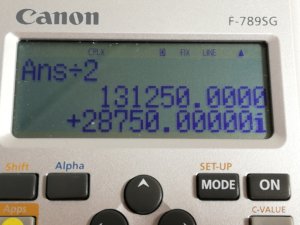
28750.00となります。これがABCDの地積です。
簡単に面積を出す方法
ちなみに、もっと簡単に出す方法もあります。
公式はこんな感じ。
Conjg(A-C)(B-D)=倍面積
この方法は対角線上に座標がある場合のみに使える方法です。
実際に出してみます。
これも倍面積なのでそのまま[÷] [2] [=]してください。
下の段の数字が28750・・・になればOKです。
面積計算についてはこちらで詳しく解説しています。
参考:【土地家屋調査士】関数電卓[F-789SG]の使い方|面積計算(複素数)

交点計算の方法

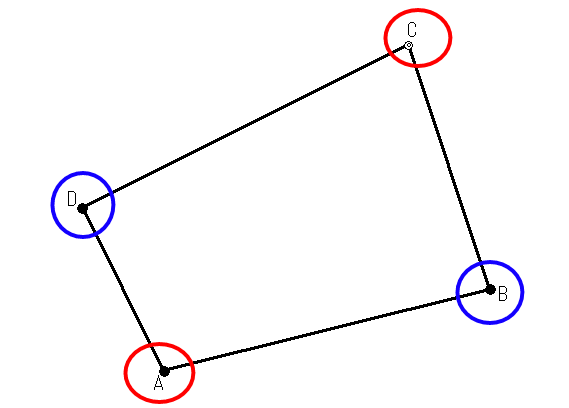
交点計算とは、直線と直線の交点の座標(未知点)を求めることです。
上の画像で言うと既知点(すでに座標が分かっている点)を結んだ線によって交点ができていますね。
交点計算はかなり複雑です。
今まではCPLXモードを使っていましたが、交点計算ではSTATモードとEQNモードの合わせ技で解きます。
詳しくはこちらで解説しています。
参考:【土地家屋調査士】関数電卓[F-789SG]の使い方|交点計算の方法

私のサイトではキャノンの関数電卓を使った方法を紹介していますが、こちらのサイトではカシオを使って計算する方法を紹介しています。
キャノンでもカシオでも計算の手間はほとんど同じです。
私はメインの計算をキャノン、サブ(交点計算)でカシオを使っていました。このあたりはお好みでどうぞ。
さて、今回の記事はここまでです。
関数電卓の使い方をマスターしたら、次は数学の公式を覚えましょう。

使用するテキストを知りたい人はこちらをどうぞ。
参考:《独学OK》土地家屋調査士試験に合格するためのオススメのテキストまとめ



