土地家屋調査士試験では「交点計算」をするって聞いたんだけど・・・
そもそも交点計算って何?どうやって計算するの?
このような疑問にお答えします。
調査士試験では交点計算が頻出です。絶対にマスターするべきテクニックですね。
今回はF-789SG-SL(キャノン)を使って交点計算をする方法をご紹介します。
(※F-789SG-SL=F-789SGのことです。新しいバージョンにはSLがついています。これ以降、SLの表記を省略します)

この記事を書いている私は現役の土地家屋調査士です。半年の独学で試験に一発合格しています。
交点計算とは?

交点計算とは、直線と直線の交点の座標(未知点)を求めることです。
上の画像で言うと既知点(すでに座標が分かっている点)を結んだ線によって交点ができていますね。
赤い線と青い線が交わる部分のことです。この交点の座標を求める計算をこれからやっていきます。
注意点
F-789SGの仕様上、通常計算で使用する「CPLXモード」を交点計算で使用する「STATモード」に変換してしまうと、「CPLXモード」で予め記録したメモリーのY座標が消えます。
なので、通常計算用の関数電卓と交点計算用の関数電卓は分けたほうがいいです。同一機種でもいいので、1台しか持っていない人はもう1台買っておきましょう。
(※Y座標が削除される現象の回避策があるかもしれませんが、私自身は専門家ではありませんので詳細はメーカーに直接お問い合わせしてください)
交点計算をする前の設定
メモリーのリセット
まずは関数電卓の中に残っているメモリーをリセットしておきます。

分数表示からライン表示へ変更
続いて、分数表示をライン表示(小数点)に変更します。

F-789SG(キャノン)で交点計算をする方法
(パターン①)通常の交点計算
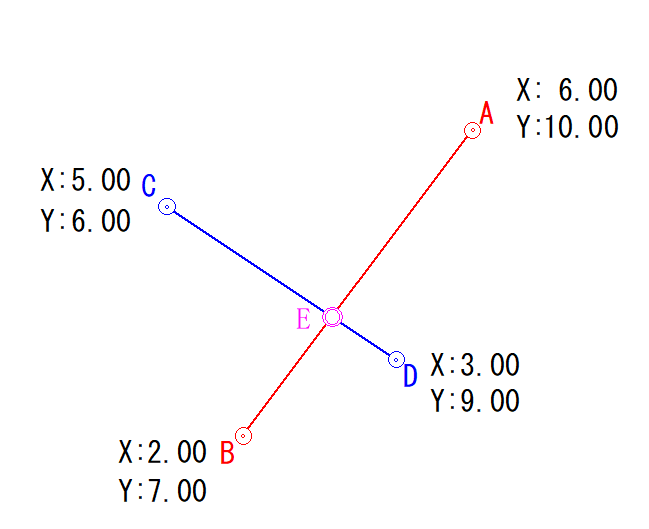
既知点ABCDがあり、直線ABと直線CDの交点がEです。
直線ABと直線CDの式をそれぞれ出して、その後に交点Eを求めます。
ところで、直線の式の公式を覚えていますか?中学校の数学で習います。
y=ax+b
aが傾き、bが切片(せっぺん)です。
これが通常の形なのですが、調査士試験の場合はちょっと違います。
Bが傾き、Aが切片です。関数電卓の仕様上、こちらの形を使うので気を付けて下さい。
計算の流れはこんな感じ。
- STATモードで直線AB、直線CDの傾きと切片を出す(それぞれメモリーする)
- EQNモードで直線AB、直線CDの交点を出す
STATモードで直線AB、直線CDの傾きと切片を出す
直線の式はSTATモードで出すことができます。※[MODE]は一番上の段、右から二番目にあります。
このような画面に切り替わると思います。これがSTATモードです。
まずは、直線ABを出します。それぞれの座標を打ち込んでいきます。
| X | Y | |
| A | 6 | 10 |
| B | 2 | 7 |
電卓のボタンの配置はこちら。

数字を打ち込んだら[=]を押すと確定できます。
[=]を押すと右の行ではなく、下の段に移動するので矢印ボタンで打ち込みたい場所までカーソルを移動させてください。
このような状態になればOKです。

慣れてくるとまずはX座標を全部打ち込んでからY座標を打ち込む・・・というテクニックも使えるようになりますが、ミスりやすいので気を付けて下さい。
あと、もしも打ち間違えたら、ミスしたところにカーソルを合わせて[DEL]キーを押せば消えます。
[CA]を押すと初期画面に戻るので注意。
先ほどの画面のままの人はいったん、[CA]を押して初期画面に戻ります。
続いて、傾きと切片を出します。
まずはA(切片)から出して、それをメモリーします。


[=]より前の操作で切片を出しています。[=]を押すと5.50と出るはずです。
[=]より後の操作で出した切片の値を[A]に記録しています。
続いてB(傾き)を出します。
先ほどとほとんど同じです。[=]を押すと0.75と出るはずです。
今度は[B]に記録させます。
傾きと切片をそれぞれ計算して関数電卓にメモリーしたってことですね。
ここまでで直線ABの式が出せました。
さて、次は直線CDを出します。
まずはSTATモードを起動します。やり方はさっきと同じ。今度は切片をC、傾きをDに記憶させましょう。
このような画面に切り替われば成功です。

続いて、CとDの座標を打ち込みます。
| X | Y | |
| C | 5 | 6 |
| D | 3 | 9 |
[CA]を押して初期画面に戻ります。
次に傾きと切片を出します。やり方はさっきと同じですが、関数電卓の表示上ではA=切片、B=傾きになっています。
AとBのメモリーは直線ABの計算の時に使ったので、今回は傾きをD、切片をCに入れます。分かりにくいのでミスしないように注意です。

まずは切片から出して、それをCのボタンにメモリーします。(切片は13.50です)
続いて傾きを出して、Dにメモリーします。(傾きは-1.50になります)
EQNモードで交点の座標を出す
ここまでの計算で直線ABと直線CDの式が出せました。
下の画像だと赤い線と青い線の式を出したところです。
- 直線ABの式:-BX+Y=A
- 直線CDの式:-DX+Y=C
ここから交点E(ピンクの点)を出していきます。

交点を出す際に使うのは「EQN」モードです。さっそく起動してみます。
このような画面になりますね。

ここで、直線の公式を思い出します。
この形でしたね。今回計算した値を当てはめるとこんな感じ。
- 直線ABの式:-BX+Y=A
- 直線CDの式:-DX+Y=C
先ほど起動したEQNモードでは
aX + bY = c という形になっています。つまり
| a(X) | b(Y) | c | |
| 1 | -B | 1 | A |
| 2 | -D | 1 | C |
こうなりますね。(Yの前には一見すると何もありませんが数字の1が隠れています。※1×Yの1が省略された形です)
これらをそれぞれ打ち込んでいきます。(aの欄にはマイナスがつくことに注意)
これで一段目が入力されていますね。続いて二段目です。
二段目の入力が終わりました。画面はこのようになっています。

続けて、[=]を押すとX座標が表示されます。
X=3.56です。(32」9と表示される人は[F←→D]ボタンを押してください)
続けて、[=]を押すとY座標が表示されます。
Y=8.17です。
これで、直線ABと直線CDの交点であるEの座標が出ました。
答え:E(3.56 , 8.17)
これが基本の形です。最初は難しいですが何度も解けばすらすら解けるようになります。
(パターン②)直線の式との交点の場合
Xの座標値が同じパターン

ここからは応用編。このパターンもよく出ます。
直線ABは先ほどと同じ式です。
ここで直線DFに注目してください。
| X | Y | |
| D | 3 | 9 |
| F | 3 | 6 |
それぞれのXの値が同じですね。このようなパターンでは先ほどのようにSTATモードで直線DFの式を出すことができません。
ですが、直線DF上に交点Gがあるので、GのX座標も3だということが分かりますね。
G:X=3、Y=?
こんな感じ。Xの座標はすでに分かっているのであとはYを出すだけです。
ここで先ほどの直線ABの式が出てきます。
-BX+Y=A
変形すると
Y=A+BX
になります。(-BXを右側に移項。※移項すると符号が変わります(+は-、-は+になる))
ここで、AとBとXの値はすでに出ていますね。AとBの値はさっきSTATモードで出しています。
すでに関数電卓に記憶させているのでそのまま使えます。
A=切片、B=傾き、X=3です。
では、Yを出しましょう。
EQNモードのままになっている人は複素数モードに切り替えます。
次に、Y=A+BXの式に当てはめていきます。

7.75と出ればOKです。
答え:G(3, 7.75)
Yの座標値が同じパターン
先ほどはX座標が同じ場合のパターンを紹介しました。
| X | Y | |
| D | 3 | 9 |
| F | 3 | 6 |
↑この場合はYの座標が知りたいので-BX+Y=AをY=A+BXに変形しましたね。
逆にY座標が同じパターンでも使えます。
| X | Y | |
| D | 9 | 3 |
| F | 6 | 3 |
Yの座標が同じです。つまりY=3です。
この場合はX座標を求める必要があるので
-BX+Y=AをX=●●の形に変形します。こっちの変形はちょっとめんどくさいです。
できれば完成形を丸覚えしたほうがいいです。
- -BX+Y=A
- BX-Y=-A《すべての値に×(-1)をして符号を変えた》
- BX=Y-A《Yを移項した》
- X=(Y-A)÷B《両辺をBで割った。この式を丸覚えしよう》
この式に当てはめていきます。※[ ( ]と[ ) ]は数字の9の上あたりにあります。
※[-]は[=]の隣にある普通の引き算です。[(−)]ではないので注意。

-3.33と出れば正解です。
答え:(-3.33 , 3)
今回の記事は以上です。
注意点ですが、今回紹介した方法はF-789SG(キャノン)で交点計算をするやり方です。
カシオを使う場合はやり方が違うので気を付けてください。
他の計算方法についてはこちらの記事でまとめています。
参考:【土地家屋調査士】複素数を使って最短で試験に合格する方法|F-789SG-SL(キャノン)