今回は地積を出してみます。
地積とは土地の面積のことですね。
土地家屋調査士試験の問題では申請書に地積を記入する欄があるのですが、この数値は自分で計算する必要があります。
たいてい、他の計算をした後、つまり必要な座標値を全て出した後に計算をすることになります。
なので、距離、方向角、座標値の出し方がマスターできていない人はまずはそちらの復習をしてください。
参考：【土地家屋調査士】複素数を使って最短で試験に合格する方法｜F-789SG-SL（キャノン）
使う電卓はF-789SG（キャノン）です。ではやってみましょう！
座標値を関数電卓に記憶させる
まずはいつも通り、座標値を電卓のメモリーに入れます。今回は面積計算なので4つの座標を入力します。座標入力の方法が分からない人はこちらを見て下さい。
| A | 100 | 100 |
| B | 150 | 300 |
| C | 300 | 250 |
| D | 200 | 50 |
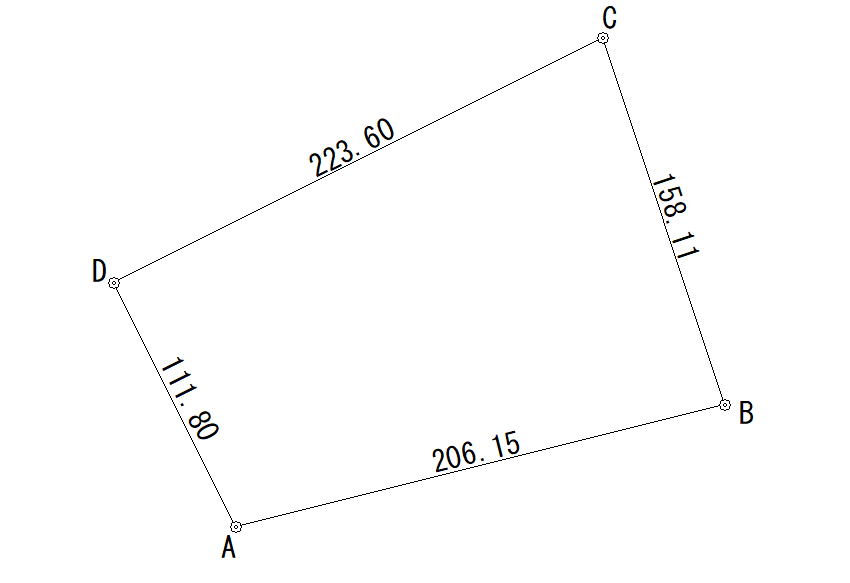
位置関係はこのようになります。
フル桁に戻す
ここで注意点です。地積の計算では小数点以下第3位を切り捨てた数値を記入します。四捨五入ではなく、切り捨てです。距離を解答欄に書く場合と同じですね。
例えば、123.456789㎡という答えが出たら、申請書には123.45㎡と書きます。（宅地の場合）
宅地以外の雑種地や田、畑などの場合は小数点以下は全て切り捨てます。なので123㎡になりますね。四捨五入ではなく、切り捨てです！よく間違えるので注意です。
ということで関数電卓の設定をフル桁に戻しておきます。
面積計算の基本パターン
まずはどんな形の土地であっても計算できる方法です。かなりめんどくさいので入力ミスがないように気を付けて下さいね。
面積計算をする場合に使うのは「Conjg」という関数です。Apps→4：Conjgで出ます。公式としては以下のようになります。
Aから始まり右回りにぐるっと一周します。まずAと打ったらConjgの中に入れるのは次の点であるBです。次はBから始まりConjgの中にCを入れます。最後はDから始まり、Conjgの中にはAを入れて最初に戻ってきます。
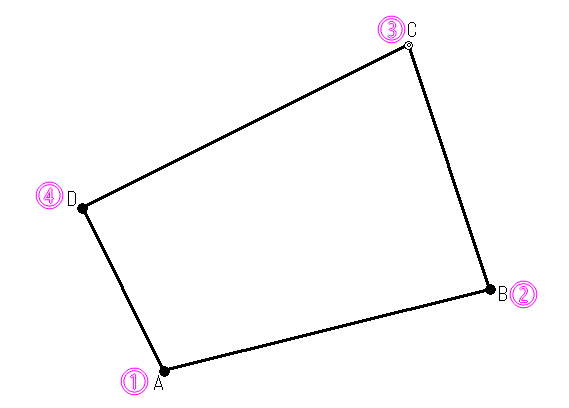
実際に計算してみましょう。以下のように電卓を叩いてください。[ ) ]を忘れないように気を付けて下さいね。一番最後のみ省略しても大丈夫です。（Aの後）
このような数字が出ると思います。倍面積は下の段の57500.0000です。上の段の262500.00は関係ないので無視でOK。その計算画面のまま、 [÷] [2] [＝] と押します。
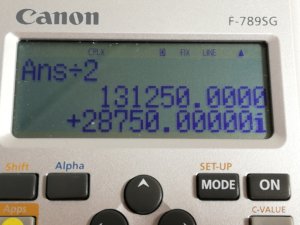
28750.00となります。これがABCDの地積です。申請書に書く数字になります。ちなみに、地積で使う数字の前に「−」がついても無視していいですよ。数字だけを見て下さい。
それから今回はAから始まりDで終わっていますが、順番を守ればどこから始めてもいいですよ。Bから始まりAで終わってもいいし、Dから始まりCで終わっても良いです。
また、右回りでなくとも左回りで計算しても同じ結果が出ます。A→C→D→Bみたいに順番がバラバラでなければ、スタートはどこでもいいし、反時計回りでもOKということです。
対角線上に座標がある場合の面積の求め方
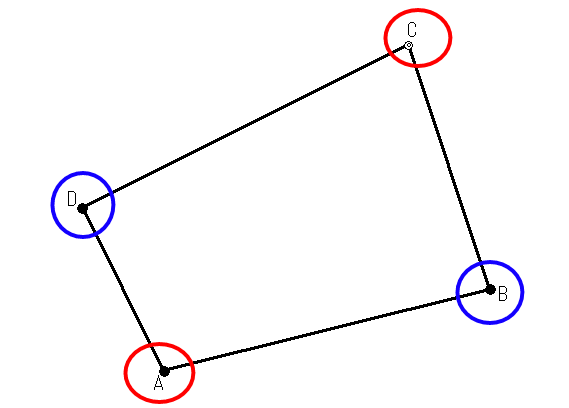先ほどのパターンはどんな形の土地でも計算できるのですが、計算が複雑でとってもめんどくさいですよね～。これから紹介する方法は対角線上に座標がある場合のみに使える方法ですが、先ほどのやり方よりはかなり楽なのでご紹介しておきます。
今回の土地の形は四角形です。なので対角線を結ぶことができますね。四角形だけでなく、点の数が偶数の場合はこれから紹介する方法が使えます。
式はこのようになります。
これも倍面積なので [÷] [2] [＝] 28750㎡となります。ちなみに()の中の順番は何でもいいです。（C－A)(D－B)でも同じ数字がでます。座標の順番を入れ替えると地積の結果に「−」がつくことがありますが、先ほど説明したとおり無視して大丈夫です。
三角形の場合の面積の求め方
ちなみに三角形の場合はちょっとやり方が違います。三角形ABCの面積を出してみます。まずは、基準となる点を決めます。今回は「A」でいきましょう。
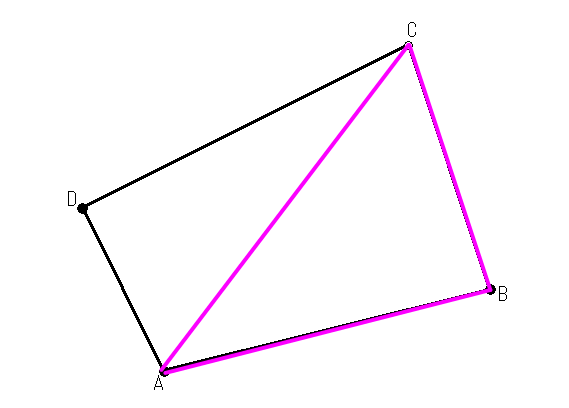
これも倍面積なので [÷] [2] [＝] とします。答えは16250.00㎡です。先ほどの四角形のパターンと同じで(A－B)(A－C)の部分を(B－A)(B－C)または(C－A)(C－B)としてもいいです。
基準とした点から他の点をマイナスするということですね。ちなみに(A－B)(A－C)の場合だと(B－A)(C－A)という風に基準点を後から引くパターンでも同じ計算結果が出ます。
どちらのやり方でも答えは同じなので、自分に合うやり方でやってみてください。
補足：求積表の練習は必要？
土地家屋調査士試験の土地の図面では求積表を書く練習をしますね。
もちろん、求積表が全く書けないのはマズイですし、計算方法も一応は知っておいた方がいいです。
ですが、実際に本試験の問題に出題されるのはごく稀です。
ここ15年くらいは求積表を書かせていないんじゃないですかね？
あれはほぼ作業みたいなもので、電卓の打ち間違いさえしなければ誰でも書けます。
なので試験でもあまり出されることはないんですよね。
求積表で地積の計算をするのはとても時間がかかるので、今回紹介した複素数計算で出した方がいいです。
とは言っても、絶対に出ないとは限らないので10回に1回くらいは求積表を書く練習をしておいた方がいいかもしれませんね。
さて、今回の記事はここまでです。
他の計算方法についてはこちらを参考にしてください。
参考：【土地家屋調査士】複素数を使って最短で試験に合格する方法｜F-789SG-SL（キャノン）
