今回は関数電卓F-789SG（キャノン）を使って方向角を出していきます。
こちらの記事は筆界点間の距離の出し方をご紹介しましたが、方向角の問題も頻出です。
参考：【土地家屋調査士】関数電卓[F-789SG]の使い方｜二点間距離の求め方（複素数）
土地家屋調査士試験では方向角の出し方は基礎の基礎です。必ずマスターしましょう！
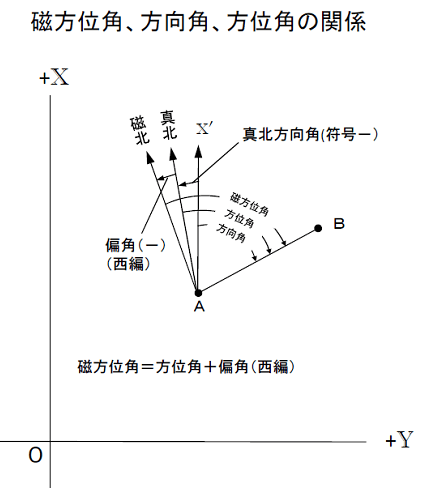
方向角と方位角の違い
出典：国土地理院
- 磁北…方位磁石が指す「北」のこと。この北を基準にして右回りに測った角度を磁方位角という。
- 真北…北極点、つまり地球の自転軸の北端（北緯90度地点）を指す方位。つまり普通の「北」のこと。この北を基準にして右回りに測った角度を方位角という。
- 座標の北（方眼北）…平面直角座標のX軸（縦軸）を0度（北）として右回りに測った角度のこと。この北を基準にして右回りに測った角度を方向角という。
測量士補の勉強をしたことがある人なら聞いたことがあるかもしれません。
土地家屋調査士試験で使うのは主に座標の北を基準にした方向角です。
座標上で計算をするので当たり前ですね。念のため言っておきますが、これらの定義は無理して覚えなくても良いですよ。
方向角以外はほとんど出ないので、一応軽く目を通すくらいで大丈夫です。
たまに引っ掛け問題で方位角が出てくることがあるので、その場合は注意です。
F-789SG（キャノン）で方向角を出す方法
座標入力をする
まずはいつも通り座標を入力します。T1、T2の座標を[A]と[B]に記憶させておいてください。
やり方が分からない人はこちら。
参考：【土地家屋調査士】関数電卓[F-789SG]の使い方｜座標入力・メモリーの方法（複素数）
| X | Y | |
| T1 | 100 | 100 |
| T2 | -150 | 200 |
方向角の出し方
T1からT2の方向角
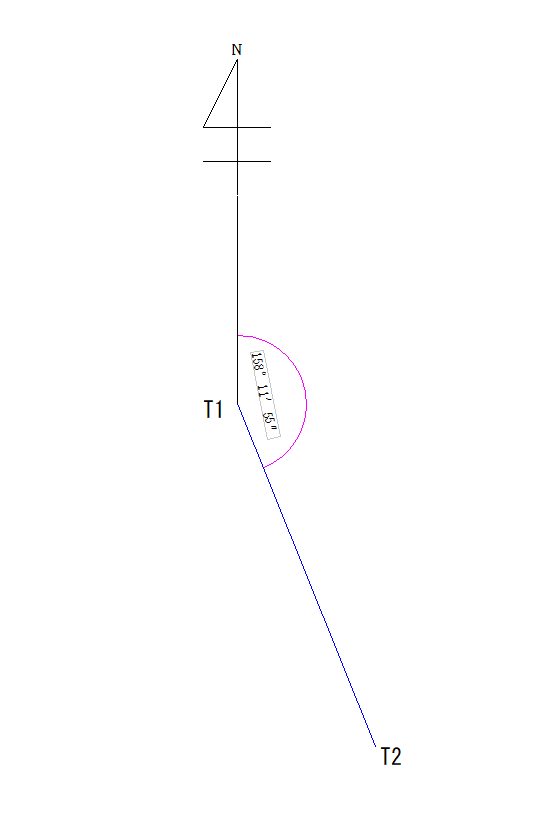今回出したいのはピンクの角度ですね。関数電卓で出す場合はこのように打ち込みます。
Appsを押すと計算メニューが出てくると思いますが、「3：Arg」を選択します。
答えは158.1985905となり、[°′″]を押すと158°11′54.93″となります。（[°′″]は画像ではBのボタンと同じ位置にあります）
ちなみに方向角は「秒止め、四捨五入」です。
つまり158°11′54.93″は0.93″を四捨五入して158°11′55″になります。
筆界点間の距離と違い、方向角は途中計算の段階で丸めていいです。
※ [Alpha]を[RCT]に置き換えても計算できます。
注意点ですが、T1からT2の方向角を計算する場合は、T2－T1になります。方向角は後ろから前を引くという風に覚えておきましょう。
T2からT1の方向角
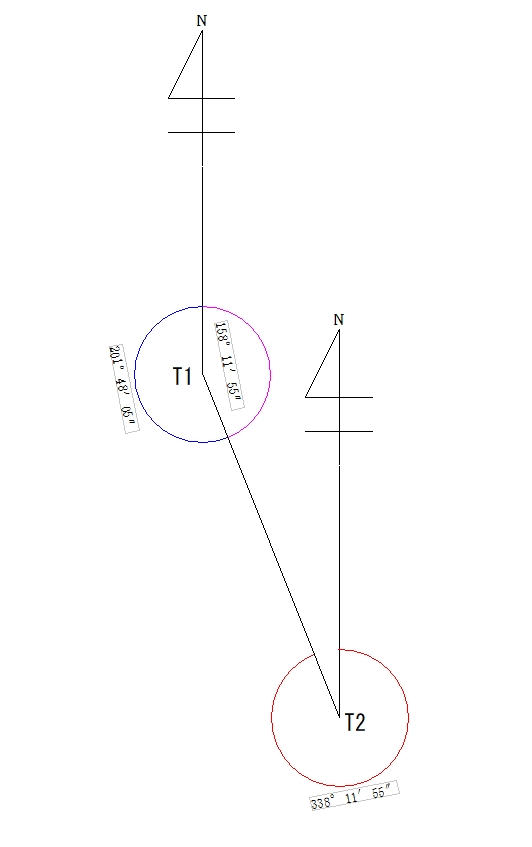では、今度はT2からT1の方向角を出してみます。画像の赤の部分です。
青い部分ではないので気を付けてくださいね。
（補足）180°を足したらどうなる？
先ほどT1からT2の方向角を計算しましたが、答えは158°11′55″でしたね。
これに180°を足すと338°11′55″になります。
T2からT1の方向角になりますね。 逆に338°11′55″から180°を引けばT1からT2の方向角が出ます。 図にするとこのようになります。
ピンク…T1→T2の方向角、赤…T2→T1の方向角です。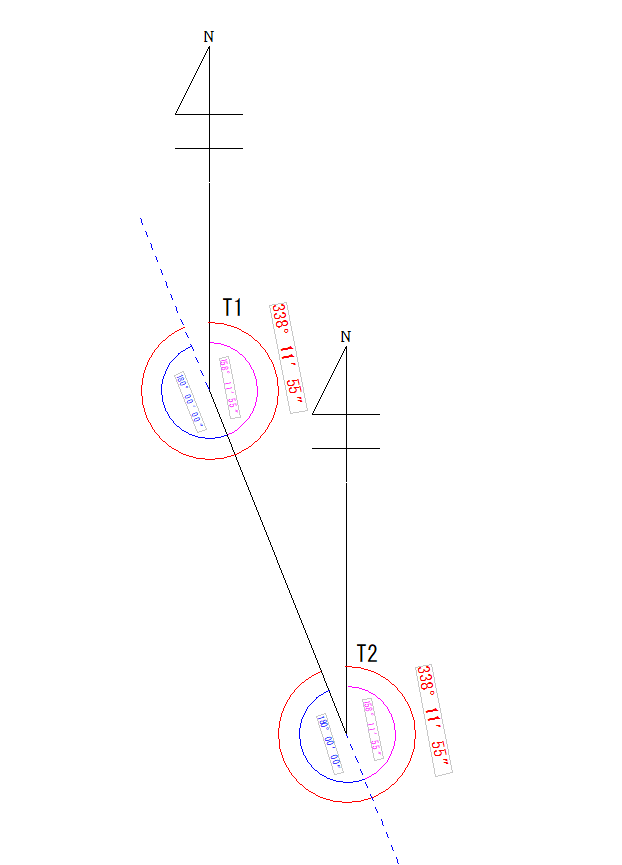 
この考え方は調査士試験の土地の問題でよく見かけます。
最初は頭が混乱して理解できないかもしれませんが、基本のこの形を覚えておけば、いずれスラスラとけるようになりますよ。
アークタンジェント(tan-1)を使った方法
筆界点間の距離の出し方と同様で、方向角にも複素数を使わずに出す方法があります。
たまに解説で見ることがあるのでご紹介しておきます。
複素数を使った方が計算が早いしミスをしにくいので、軽く目を通すだけで大丈夫です。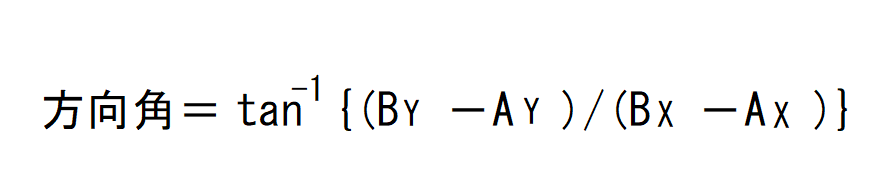
tanに－1がついているものは「アークタンジェント」と読みます。
Shittを押した後にtanを押せば入力できます。
カッコの中がちょっとめんどくさいですね。AB表示だと分かりにくいのでT1、T2をこの公式に当てはめてみます。
| X | Y | |
| T1 | 100 | 100 |
| T2 | -150 | 200 |
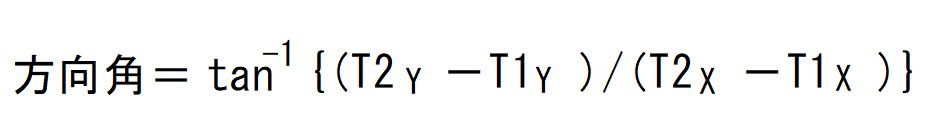
今回はT1→T2の方向角を出すのでT2－T1です。
方向角は後ろから前を引くという法則は複素数を使った場合と同じですね。
カッコの中は（Y座標同士を引いた数）÷（X座標同士を引いた数）ですね。
T1とT2の順番が入れ替わるとT1→T2の方向角ではなくT2→T1の方向角になるので気を付けて下さいね。
電卓ではこのように打ち込みます。
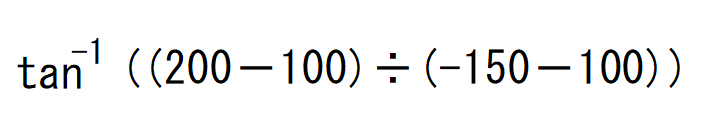
-28°48′5.07″と出ると思います。この数字に180°を足すと158°11′54.93″と出ますね。
先ほど複素数で出した答えと同じです。T2は第二象限の点なので最後に「180°」を足します。
※第二象限の意味が分からない人はこの本を読んでください。
こちらの本にこの解き方の詳しい説明が載っています。
複素数の方が計算は早いのですが、数学的な知識としてアークタンジェントを使った公式の意味も知っておいた方がいいです。
サラッと読む程度でいいので一応目を通しておいてくださいね。
さて、今回は関数電卓を使った方向角の出し方をご紹介しました。土地の問題で必ず一回は計算するので必ずマスターしておいてくださいね。
他の計算方法はこちらでまとめています。
参考：【土地家屋調査士】複素数を使って最短で試験に合格する方法｜F-789SG-SL（キャノン）
