
土地家屋調査士試験の午後の部(記述式)は、とにかく時間が足りません。
「計算ミスをした」「最後まで解ききれなかった」という受験生が後を絶たないのが現実です。
なぜ、多くの受験生が「複素数モード」を使うのか?
理由はシンプルで、「圧倒的に計算が速くなり、記述式試験で逃げ切れるから」です。
通常の方法で計算していては、合格レベルのスピードには到達できません。
「複素数って何? 虚数iって何?」と数学的な定義を覚える必要は一切ありません。
「関数電卓のボタンをどう押せば、答えが一発で出るか」だけを覚えればOKです。
私自身、この「Canon F-789SG」を使い倒し、半年の独学で一発合格を勝ち取りました。
この記事では、土地家屋調査士試験で必須となる関数電卓 F-789SG の「設定リセット」「丸め」「メモリー」「複素数モードの使い方」から、二点間距離、方向角、面積計算、座標計算、交点計算まで“試験本番で必要な全操作” をまとめて解説します。
この記事を読めば、これまでバラバラだった複素数計算の手順がすべて1つの記事で完結します。
読み終えれば、あなたの計算スピードは劇的に上がります。
▼ 動画で操作を確認したい方はこちら
F-789SG-SL(キャノン)の基本設定(リセット)
設定を全てリセットする

これは関数電卓の設定を初期設定に戻す方法です。
これから関数電卓の設定を色々変えていくのですが、自分がどんな設定にしているかが分からなくなった場合などに使ってください。
普段は次に紹介するメモリーのリセットだけで大丈夫です。
メモリーをリセットする

先ほどは設定全てをリセットしましたが、今後はメモリーのみをリセットします。
後から解説しますが、関数電卓は計算で出した数字を電卓内に記録(メモリー)することができます。
なので、新しい問題を解く前に、この作業を行うことによって、関数電卓に記録されている数字を全て消すことができます。
この作業を怠ると、前の問題で使った数字を間違って使ってしまい、計算ミスを起こす原因になるので気を付けて下さいね。
問題を解き始める前にこの作業は必ず行ってください。
分数表示からライン表示へ変更

関数電卓には分数教示とライン表示の二種類があります。
ライン表示というのは少数点で表示することですね。たとえば3÷2を関数電卓で計算するとこのように表示されます。
- 分数表示…3 」2(=3/2ということです)
- ライン表示…1.5
調査士試験では小数点で解答するので関数電卓の表示自体を変えておきます。
ちなみに、「F←→D]というボタンを押せば分数表示←→ライン表示の切り替えができます。(DELボタンの上にあります)
この設定をすると画面の上に「LINE」という文字が表示されます。
表示されていない場合はもう一度押し直しましょう。
小数点以下の表示範囲の設定
小数点以下第2位までの表示にする
『座標値は計算結果の小数点以下第3位を四捨五入し,小数点以下第2位までとする』という公式の指示があります。
(※問題に載っている座標値は全てメートル単位です。0.01m=1cmということですね)
例えば座標値がX=1.1111、Y=.2.2222だったらX=1.11、Y=2.22になりますね。
では、X=1.135、Y=2.268だったらどうなるでしょうか。
正解はX=1.14(5を四捨五入)、Y=2.27(8を四捨五入)になりますね。
この数字を解答欄に書いたり、後で紹介する求積の際に使用します。
関数電卓の初期設定ではフル桁(=小数点以下第9位)の表示になっています。
計算のたびに「えっと、5を四捨五入して繰り上がるから~1.135は1.14だな!」という風に考えるのはメンドクサイんです。
なので、関数電卓の表示も小数点以下第3位を四捨五入した、小数点以下第2位までの表示にします。

最後の[2]の部分で小数点以下第2位までの表示にするという設定をしています。小数点以下第3位までの表示にしたいなら
とすれば良いということですね。さて、先ほどの小数点第2までの表示に戻して1÷6を計算してみてください。答えは「0.17」になるはずです。そのままの状態で再びフル桁に戻してみます。
計算結果は残したままで、同じように打ち込んでみて下さい。
最後に[9]を押すことでフル桁に戻せます。答えは「0.166666667」となるはずです。
小数点以下第2位の表示では「0.166666667」を四捨五入しているので画面上では「0.17」と表示されます。
※表示範囲をフル桁以外にすると画面上に「FIX」文字が追加されます。
注意点
基本的には小数点第2までの表示にしておいて大丈夫です。ただし、注意点があります。
先ほど、フル桁では「0.166666667」と表示された数字が小数点以下第2位の表示では「0.17」と表示されましたね。
これは画面上では「0.17」と表示されているだけです。
この表示の状態で×2などをすると、関数電卓の中では「0.17×2」ではなく「0.166666667×2」の計算結果が出ます。
あくまでも表示範囲が変わっているだけで、勝手に四捨五入された数字が記録されて計算されるわけではないので気を付けてくださいね。
この考え方は座標登録や面積計算をする際に非常に重要になってきます。
今は理解できなくてもこの後に再び説明するので安心してください。
※四捨五入することを「丸める」と言うのでついでに覚えておいてください。
複素数モードにする
最近の関数電卓では複素数が使えます。複素数の概念については非常に難しいので詳しくは知らなくてもいいです。(知りたい方は高校数学Ⅱの教科書を見てください)
関数電卓を複素数モードに切り替えれば調査士試験の土地の問題がすごく楽になります。
この計算方法を知らない人は従来の超絶メンドクサイ方法で時間をかけて計算をすることになるので大損します。必ず覚えましょう。
まずは複素数を使えるように設定をします。

MODEを押すと「2:CPLX」というのがありますね。
これが複素数モードです。(CPLX=complex number=複素数の略)
この設定をすると画面上に「CPLX」という表示が出ます。
さて、関数電卓の基本的な設定はここまでです。実際の計算の前に圧倒的に関数電卓が使いやすくなる裏技を伝授します。早く計算に行きたい!という人は読み飛ばしてOKです。
【裏技】打ち間違いを防ぐ方法
関数電卓は普通の電卓よりもボタンが多いし、ボタン同士の距離も近めです。
緊張している際にはお目当てのボタンを探すのに時間がかかったり、誤って違うボタンを押してしまったりするという予期せぬトラブルが発生する可能性があります。
ということで私は関数電卓のよく使うボタンにはシールを貼ったり、滑り止めの液を塗っています。(下の画像の赤丸部分)

私はApps、ENGに色付きのシール、DEL、+にはダイソーで買った滑り止めの液を塗って凹凸を持たせています。(本来は靴下の滑り止めとして使われる商品です)

通常の電卓でも数字の「5」の位置が少し盛り上がっていたりしますよね?
よく使うボタンなので指で触れた感覚でどのボタンを押しているのかを分かるようにしています。
また、電卓カバーにはカーペットの裏に貼る滑り止めを貼っています。
テーブルの上に電卓を置くと滑るんですよね。ボタンがとても打ちにくいのでこのような予防をしています。見た目は悪いですが打ち込みやすくなるのでオススメです。

座標値を入力する方法(メモリー)
さて使い方の続きです。
まずは座標値入力の方法からです。土地の計算を始める前に問題文に載っている既知点の座標を関数電卓に記憶させます。(メモリーする、という言い方もします)
| X | Y | |
| T1 | 100 | 100 |
| T2 | -150 | 200 |
まずはT1から入力してみます。X=100、Y=100ですね。関数電卓ではこのように入力します。

ボタンが多くて探しにくいと思うので、数字や+以外の場所に印をつけています。頑張って探してくださいね。手順通りに進むとこのような画面になるはずです。

①100+100iを入力。関数電卓で数字を座標として入力したい場合にはXとYをこのように打ち込みます。見慣れないと思いますが、これから何度も出てくるのでいずれ慣れます。

② [shift] [STO] [A]を入力。これは先ほど打った座標をAというボタンに記録させますよ、という意味です。(STO=ストックですね)
続いてT2も入力します。X=−150、Y=200ですね。「−(マイナス)」の打ち方ですが、÷の下にあるのは引き算で使うボタンです。
数字を負の数にする場合は「(−)」のボタンです。先ほどの「A」と同じ位置にあります。

※ [i] は[ON]の二つ下にあります 。私はよく使うので赤いシールを貼ってます。Bに記録できたら[CA]のボタンを押して初期画面に戻ります。
ちゃんと記録されたのかを確認したい
さて、現在、関数電卓には2つの座標が記録されているはずですね。
AにはX=100、Y=100、BにはX=−150、Y=200が保存されているはずです。
上手くできているのかを確認してみます。やり方は2通りあります。

下の画像のように表示されれば成功です。
AにはX=100,Y=100が入力されているよ~という表示ですね。Bも同様の方法で表示できます。やり方はどちらでも良いです。

RCLはおそらく「recall(リコール)」、つまり思い出すという意味ですね。Alphaについては次で解説します。
(補足)ShiftやAlphaについて
関数電卓は一つのボタンにたくさんの機能が割り振られています。
電卓の左上にShiftとAlphaというボタンがありますね。
Shiftはオレンジ、Alphaは青色で印字されています。それぞれのボタンが確認できたら他のボタンを見て下さい。
例えば先ほど押した[° ′ ″]と書かれたボタンですが、白字では「° ′ ″」と書かれていますが、その上に青字で「B」と書いてありますね。
これはAlphaを押した直後に「° ′ ″」のボタンを押せば、Bという機能を使いますよ、という意味です。
また、Bの隣にはPfactという文字もありますね。
オレンジに対応しているのはShiftでした。
なので、Shiftを入力した後に「° ′ ″」のボタンを押せば、Pfactの機能を使うことができるわけです。
関数電卓は多機能なので限られたボタンにたくさんの機能を搭載するための工夫ですね。
[F-789SG]でメモリーできるボタンはどこ?

この関数電卓はとにかくメモリーの数が多いです。
A~F+X+Y+M、あとは0~9のボタンに数値を記録することができます。
補足ですが、Mに限ってはちょっと使い方が特殊です。先ほど解説したように
で記録することもできますが、単純に[M+]を押すだけでも記録することができます。次のように入力してみて下さい。
数字にメモリーした時の表示方法
先ほど、この関数電卓は数字にもメモリー機能があると言いました。実際にやってみましょう。
二点間距離の計算方法
次は距離の計算です。
計算を始める前に先ほど使ったT1、T2の座標を[A]と[B]に記憶させておいてください。
(間違えて消した人のために再掲しておきます。もう一度、座標値の入力を復習したい人はこちら)
| X | Y | |
| T1 | 100 | 100 |
| T2 | -150 | 200 |
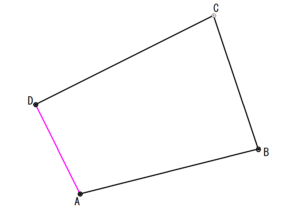
では、T1とT2の距離を求めてみましょう!図でピンク色の線の部分です。

距離は[Abs]を使い求めることができます。

答えはフル桁だと269.2582404となります。
小数点以下第3位を四捨五入した数値は269.26となります。
ちなみに計算した辺長を次の計算で使う場合は、フル桁のまま使っても、四捨五入した値を使っても答えに大差はないです。
こちらで詳しく解説している先生がいるので参考にしてください。
参考:早くて正確に!複素数による測量計算ミニ講座③特殊な関数
できましたか? ※ [Alpha]を[RCT]に置き換えても計算できます。少し練習してみましょう。
練習問題
| A | 100 | 100 |
| B | 150 | 300 |
| C | 300 | 250 |
| D | 200 | 50 |
まずはこの座標を電卓に入力してください。一度メモリーをクリアにするか、先ほどのT1、T2に上書きする形で大丈夫です。
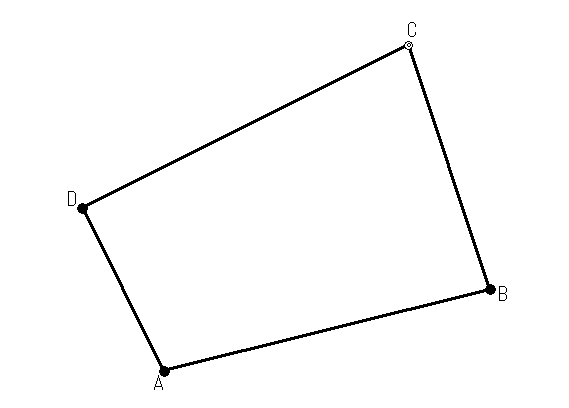
こんな感じの配置です。ではそれぞれの距離を計算してみます。
A→Bの距離
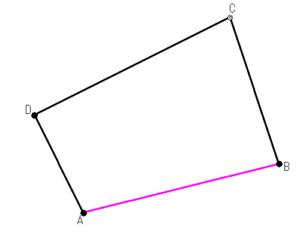
B→Cの距離
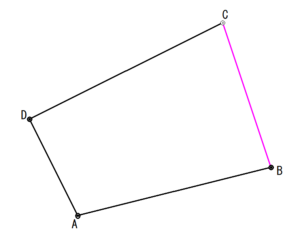
C→Dの距離
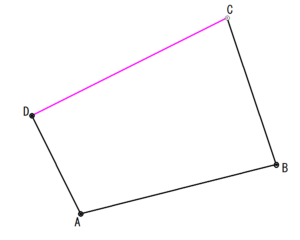
A→Dの距離
(補足)三平方の定理を使った計算方法
先ほどの計算方法は複素数を使ったものですが、三平方の定理を利用して答えを出すこともできます。
複素数を利用した方が早いのですが、テキストの解答にはこちらの方法が載っていることがあるので一応ご紹介しておきます。
例としてA→B間の距離を出してみます。
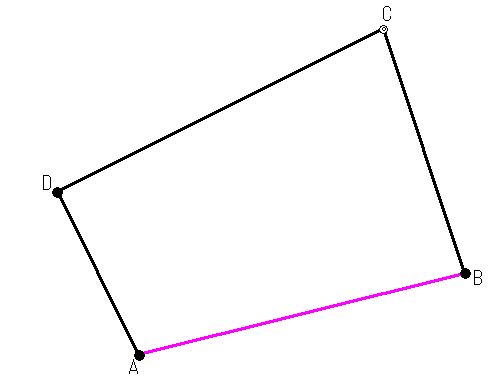
答えは206.1552813mでしたね。解き方を出す前に三平方の定理を復習しておきます。
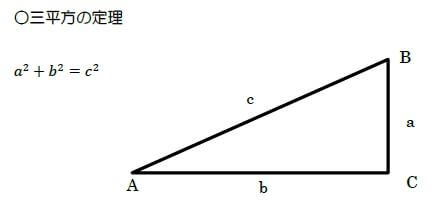
出したい部分は「c」の辺長つまり斜辺ですね。
この式を変形します。
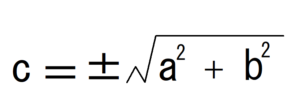
辺長は「正の数」なので「+」を採用します。答えが「−100m」なんておかしいですからね。さて、この式にAとBの座標を当てはめてみます。
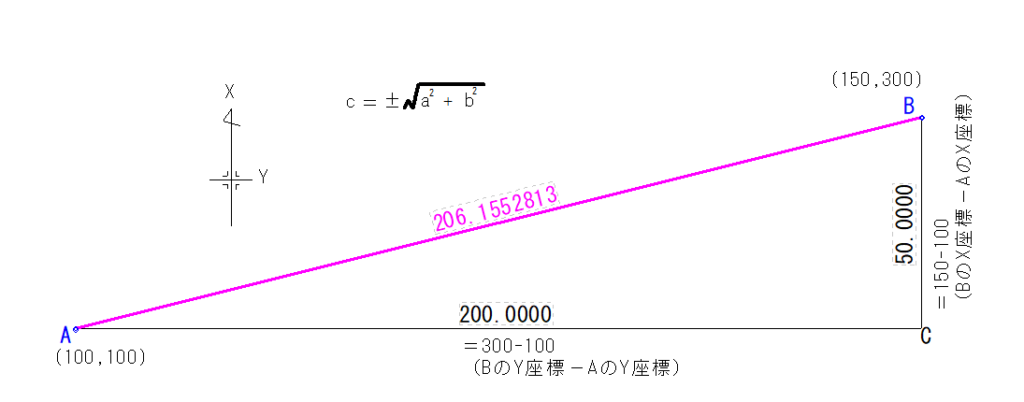
図の通り、X座標同士、Y座標同士を引いてそれを二乗しています。A-BでもB-Aでもいいです。どうせ二乗するので答えは同じです。(マイナス×マイナスはプラスになりますからね)


打ち方としてはこのようになります。この解き方は複素数を知っているならばそんなに重要ではないです。ですが、東京法経学院などのテキストを見ると解説の解き方はこちらになっていることが多いんですよね。
なので一応知っておくと良いです。距離が求められるようになったら、次は方向角の計算を押さえておきましょう。
方向角の計算方法
続いて方向角です。これもほぼ確定で試験に出ます。まずは基本的なおさらいをします。
方向角と方位角の違い
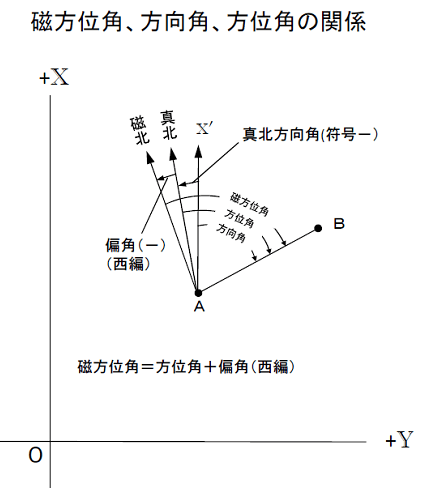
出典:国土地理院
- 磁北…方位磁石が指す「北」のこと。この北を基準にして右回りに測った角度を磁方位角という。
- 真北…北極点、つまり地球の自転軸の北端(北緯90度地点)を指す方位。つまり普通の「北」のこと。この北を基準にして右回りに測った角度を方位角という。
- 座標の北(方眼北)…平面直角座標のX軸(縦軸)を0度(北)として右回りに測った角度のこと。この北を基準にして右回りに測った角度を方向角という。
測量士補の勉強をしたことがある人なら聞いたことがあるかもしれません。
土地家屋調査士試験で使うのは主に座標の北を基準にした方向角です。
座標上で計算をするので当たり前ですね。念のため言っておきますが、これらの定義は無理して覚えなくても良いですよ。
方向角以外はほとんど出ないので、一応軽く目を通すくらいで大丈夫です。
たまに引っ掛け問題で方位角が出てくることがあるので、その場合は注意です。
座標入力をする
さて、実際に計算してみます。
まずはいつも通り座標を入力します。T1、T2の座標を[A]と[B]に記憶させておいてください。(一応再掲しますが、メモリーの操作に不安がある人はこちら)
| X | Y | |
| T1 | 100 | 100 |
| T2 | -150 | 200 |
方向角の出し方
T1からT2の方向角
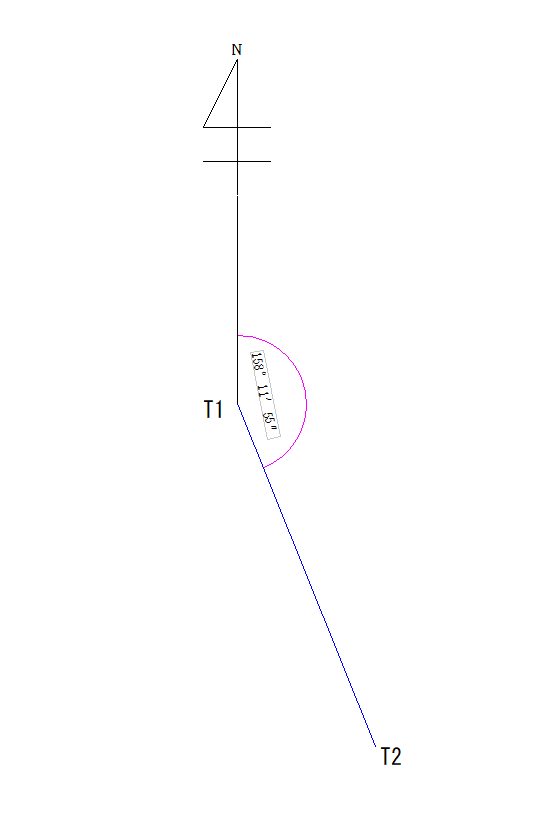 今回出したいのはピンクの角度ですね。関数電卓で出す場合はこのように打ち込みます。
今回出したいのはピンクの角度ですね。関数電卓で出す場合はこのように打ち込みます。

Appsを押すと計算メニューが出てくると思いますが、「3:Arg」を選択します。
答えは158.1985905となり、[°′″]を押すと158°11′54.93″となります。([°′″]は画像ではBのボタンと同じ位置にあります)
ちなみに方向角は「秒止め、四捨五入」です。
つまり158°11′54.93″は0.93″を四捨五入して158°11′55″になります。
筆界点間の距離と違い、方向角は途中計算の段階で丸めていいです。
※ [Alpha]を[RCT]に置き換えても計算できます。
注意点ですが、T1からT2の方向角を計算する場合は、T2-T1になります。方向角は後ろから前を引くという風に覚えておきましょう。
T2からT1の方向角
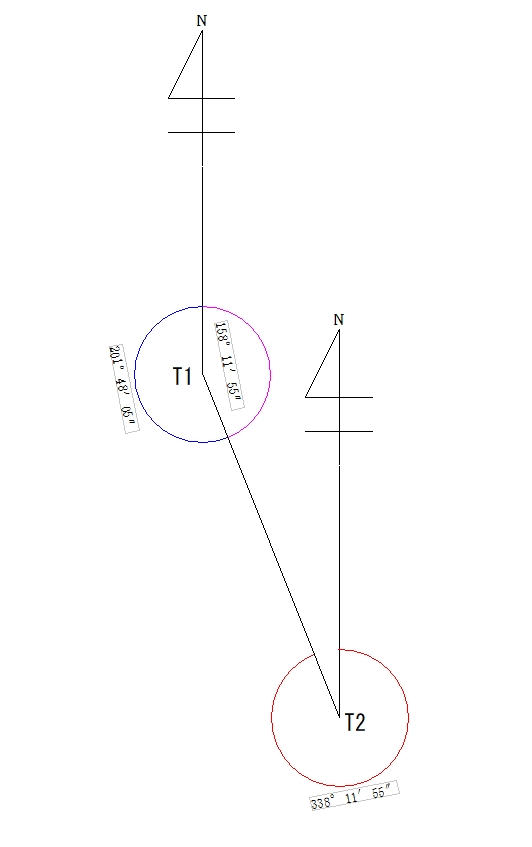 では、今度はT2からT1の方向角を出してみます。画像の赤の部分です。
では、今度はT2からT1の方向角を出してみます。画像の赤の部分です。
青い部分ではないので気を付けてくださいね。
(補足)180°を足したらどうなる?
先ほどT1からT2の方向角を計算しましたが、答えは158°11′55″でしたね。
これに180°を足すと338°11′55″になります。
T2からT1の方向角になりますね。 逆に338°11′55″から180°を引けばT1からT2の方向角が出ます。 図にするとこのようになります。
ピンク…T1→T2の方向角、赤…T2→T1の方向角です。 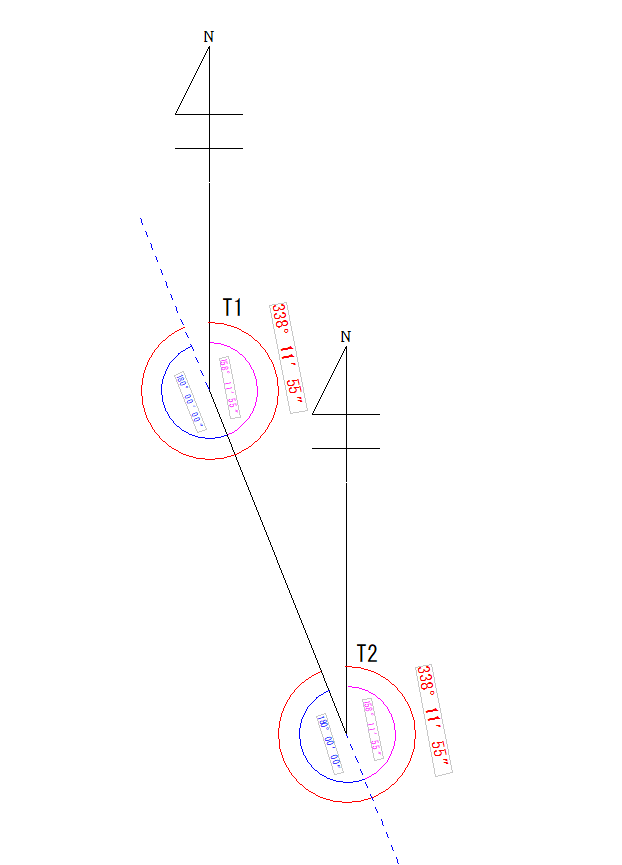 この考え方は調査士試験の土地の問題でよく見かけます。
この考え方は調査士試験の土地の問題でよく見かけます。
最初は頭が混乱して理解できないかもしれませんが、基本のこの形を覚えておけば、いずれスラスラとけるようになりますよ。
(補足)アークタンジェント(tan-1)を使った方法
筆界点間の距離の出し方と同様で、方向角にも複素数を使わずに出す方法があります。
たまに解説で見ることがあるのでご紹介しておきます。
複素数を使った方が計算が早いしミスをしにくいので、軽く目を通すだけで大丈夫です。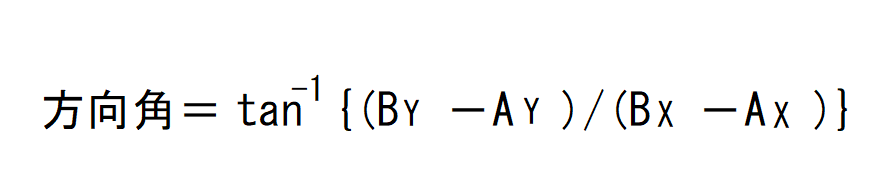
tanに-1がついているものは「アークタンジェント」と読みます。
Shittを押した後にtanを押せば入力できます。
カッコの中がちょっとめんどくさいですね。AB表示だと分かりにくいのでT1、T2をこの公式に当てはめてみます。
| X | Y | |
| T1 | 100 | 100 |
| T2 | -150 | 200 |
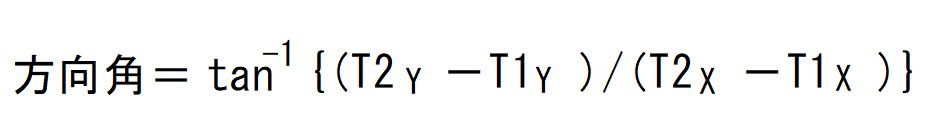
今回はT1→T2の方向角を出すのでT2-T1です。
方向角は後ろから前を引くという法則は複素数を使った場合と同じですね。
カッコの中は(Y座標同士を引いた数)÷(X座標同士を引いた数)ですね。
T1とT2の順番が入れ替わるとT1→T2の方向角ではなくT2→T1の方向角になるので気を付けて下さいね。
電卓ではこのように打ち込みます。
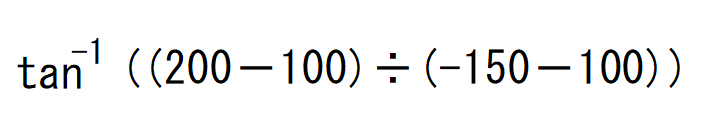
-28°48′5.07″と出ると思います。この数字に180°を足すと158°11′54.93″と出ますね。
先ほど複素数で出した答えと同じです。T2は第二象限の点なので最後に「180°」を足します。
※第二象限の意味が分からない人はこの本を読んでください。
こちらの本にこの解き方の詳しい説明が載っています。
複素数の方が計算は早いのですが、数学的な知識としてアークタンジェントを使った公式の意味も知っておいた方がいいです。
サラッと読む程度でいいので一応目を通しておいてくださいね。さて、
次は座標値です。距離や方向角の考え方が分からないと混乱するので、まだマスターしていない人は戻って復習してください。
座標値の計算方法
調査士試験の問題では大体2~3問くらいは座標値を出す問題が出てきます。
自分で計算をして出した座標値を使って地積の計算もするので、ここで計算ミスをしてしまうと大幅な減点です。 後々の解答に全て影響が出るので必ずマスターしておきましょう。
これまではT1、T2が既知点でこれらの座標値を元に距離や方向角を計算しています。
今度はT1の座標値、T1からT2までの距離と方向角が分かっている場合にT2の座標値を計算で出す方法をご紹介します。
- 既知点T1(X座標…100, Y座標…100)
- T1からT2までの距離…269.26m
- T1からT2までの方向角…158°11′55″
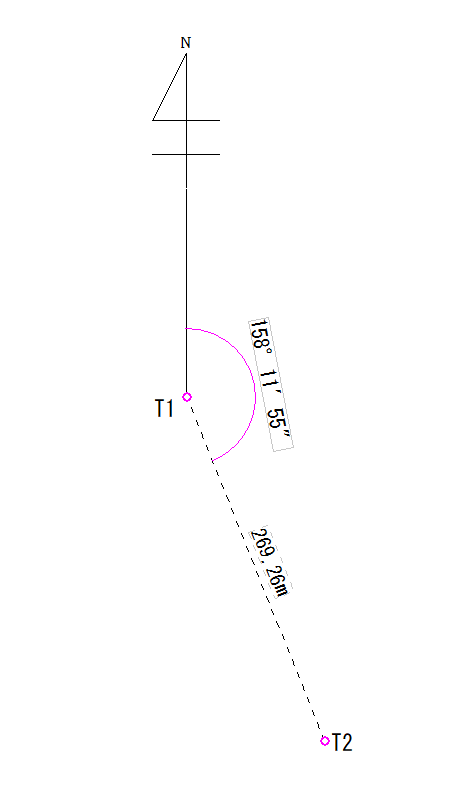 位置関係はこのような状態です。既知点T1があり、座標が不明なT2があります。このような場合に使う公式はこちらです。
位置関係はこのような状態です。既知点T1があり、座標が不明なT2があります。このような場合に使う公式はこちらです。

座標値を丸める方法
すると、X座標は-150.0016697、Y座標は200.0005636になりませんか?
『座標値は計算結果の小数点以下第3位を四捨五入し、小数点以下第2位までとする』という公式の指示があります。
普通、今回のように未知点の座標を計算で出した場合は、座標値を関数電卓にメモリーとして記憶させます。
後々面積計算をする時に必要になるからです。 ですが、計算直後の座標をそのまま記憶させてしまうと、小数点第3位以下の数字(端数)も一緒に記録されてしまいます。
X座標は-150.0016697、Y座標は200.0005636ですが、これを公式の指示通りに計算結果の小数点以下第3位を四捨五入し、小数点以下第2位までとするならX=-150.00、Y=200.00と記録しなければいけませんし、この座標を使って次の計算をする必要があります。
端数を残したままにしておくと、後の計算が微妙にずれてくるのです。
というわけで、指示通りに小数点以下第3位を四捨五入し、小数点以下第2位までの座標にします。 まずは、小数点以下第2位までの表示に戻します。
そして、もう一度先ほどの計算をしてください。(計算結果がまだ残っているなら省略可)

先ほども言った通り、今画面上では(-150.00,200.00)という座標値が表示されていますが、フル桁にすれば端数が残っているのでした。
今、小数点以下第3位を四捨五入し、小数点以下第2位までの表示になっていますが、この表示通りの座標値(X=-150.00、Y=200.00)を電卓に記憶させます。
この画面の状態でこのように打ち込みます。
そのままその座標値をBに記憶させて下さい。

このように表示されれば成功です。 今の方法を使えば、表示された数字以下を四捨五入することができます。 数字を丸める、という言い方をしますね。
座標値が出た場合は必ず毎回丸めて下さいね。 そうでないと、後からやる計算がどんどんズレていきます。
(補足)三角関数を使って座標値を出す方法
- 既知点T1(X座標…100, Y座標…100)
- T1からT2までの距離…269.26m
- T1からT2までの方向角…158°11′55″
地積(面積)の計算方法
次は地積を出してみます。地積とは土地の面積のことですね。
試験の問題では申請書に地積を記入する欄があるのですが、この数値は自分で計算する必要があります。
たいてい、他の計算をした後、つまり必要な座標値を全て出した後に計算をすることになります。
なので、距離、方向角、座標値の出し方がマスターできていない人はまずはそちらの復習をしてください。
ではやってみましょう!
座標値を関数電卓に記憶させる
まずはいつも通り、座標値を電卓のメモリーに入れます。今回は面積計算なので4つの座標を入力します。メモリーの方法は大丈夫ですか?不安な人はこちらで戻ってください。
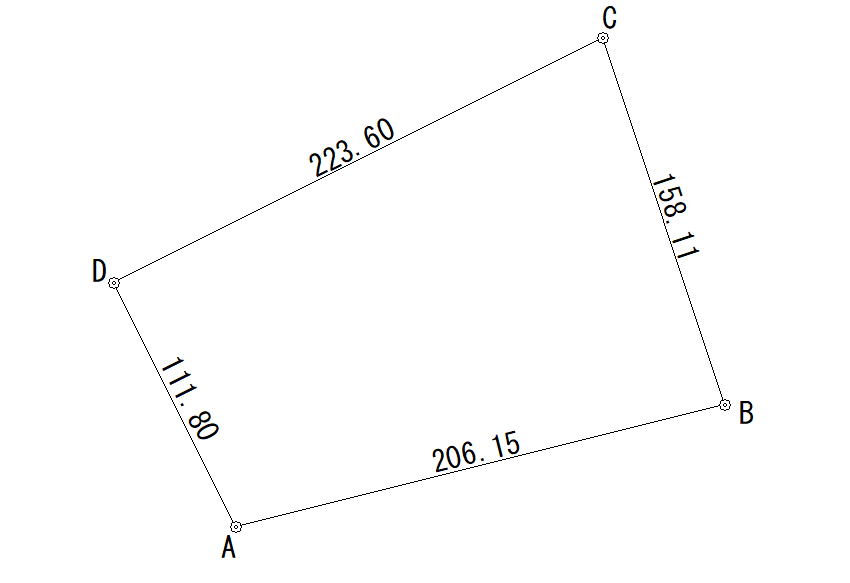
| A | 100 | 100 |
| B | 150 | 300 |
| C | 300 | 250 |
| D | 200 | 50 |
位置関係はこのようになります。
フル桁に戻す
ここで注意点です。地積の計算では小数点以下第3位を切り捨てた数値を記入します。四捨五入ではなく、切り捨てです。距離を解答欄に書く場合と同じですね。
例えば、123.456789㎡という答えが出たら、申請書には123.45㎡と書きます。(宅地の場合)
宅地以外の雑種地や田、畑などの場合は小数点以下は全て切り捨てます。なので123㎡になりますね。四捨五入ではなく、切り捨てです!よく間違えるので注意です。
ということで関数電卓の設定をフル桁に戻しておきます。
面積計算の基本パターン
まずはどんな形の土地であっても計算できる方法です。かなり複雑なので入力ミスがないように気を付けて下さいね。
面積計算をする場合に使うのは「Conjg」という関数です。Apps→4:Conjgで出ます。公式としては以下のようになります。
Aから始まり右回りにぐるっと一周します。まずAと打ったらConjgの中に入れるのは次の点であるBです。次はBから始まりConjgの中にCを入れます。最後はDから始まり、Conjgの中にはAを入れて最初に戻ってきます。
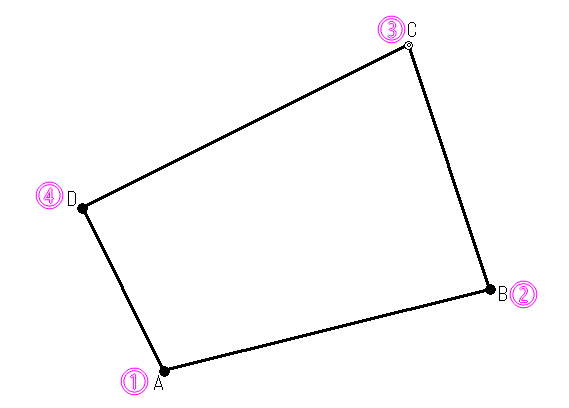
実際に計算してみましょう。以下のように電卓を叩いてください。[ ) ]を忘れないように気を付けて下さいね。一番最後のみ省略しても大丈夫です。(Aの後)


このような数字が出ると思います。倍面積は下の段の57500.0000です。上の段の262500.00は関係ないので無視でOK。その計算画面のまま、 [÷] [2] [=] と押します。
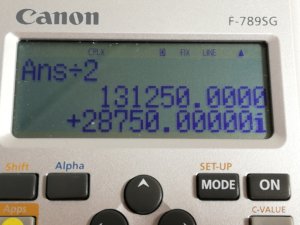
28750.00となります。これがABCDの地積です。申請書に書く数字になります。ちなみに、地積で使う数字の前に「−」がついても無視していいですよ。数字だけを見て下さい。
それから今回はAから始まりDで終わっていますが、順番を守ればどこから始めてもいいですよ。Bから始まりAで終わってもいいし、Dから始まりCで終わっても良いです。
また、右回りでなくとも左回りで計算しても同じ結果が出ます。A→C→D→Bみたいに順番がバラバラでなければ、スタートはどこでもいいし、反時計回りでもOKということです。
対角線上に座標がある場合の面積の求め方
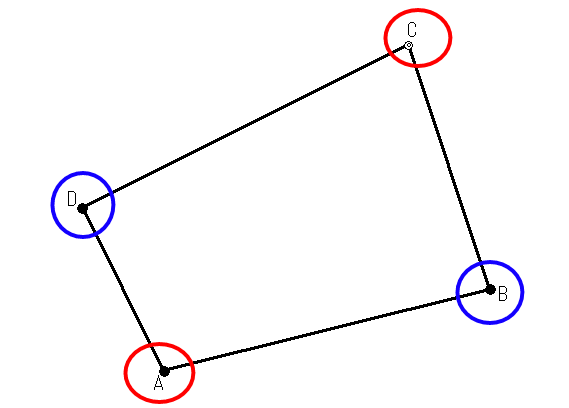 先ほどのパターンはどんな形の土地でも計算できるのですが、計算が複雑でとってもめんどくさいですよね~。これから紹介する方法は対角線上に座標がある場合のみに使える方法ですが、先ほどのやり方よりはかなり楽なのでご紹介しておきます。
先ほどのパターンはどんな形の土地でも計算できるのですが、計算が複雑でとってもめんどくさいですよね~。これから紹介する方法は対角線上に座標がある場合のみに使える方法ですが、先ほどのやり方よりはかなり楽なのでご紹介しておきます。
今回の土地の形は四角形です。なので対角線を結ぶことができますね。四角形だけでなく、点の数が偶数の場合はこれから紹介する方法が使えます。
式はこのようになります。
これも倍面積なので [÷] [2] [=] 28750㎡となります。ちなみに()の中の順番は何でもいいです。(C-A)(D-B)でも同じ数字がでます。座標の順番を入れ替えると地積の結果に「−」がつくことがありますが、先ほど説明したとおり無視して大丈夫です。
三角形の場合の面積の求め方
ちなみに三角形の場合はちょっとやり方が違います。三角形ABCの面積を出してみます。まずは、基準となる点を決めます。今回は「A」でいきましょう。
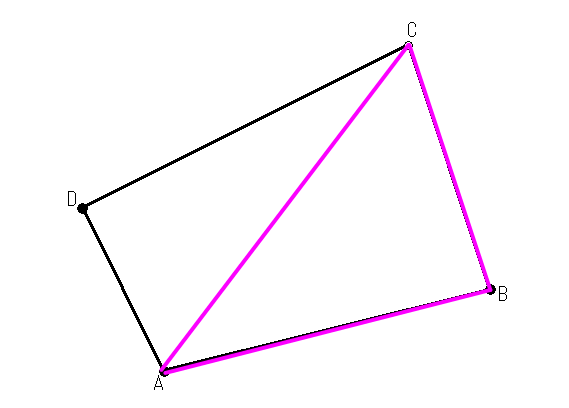
これも倍面積なので [÷] [2] [=] とします。答えは16250.00㎡です。先ほどの四角形のパターンと同じで(A-B)(A-C)の部分を(B-A)(B-C)または(C-A)(C-B)としてもいいです。
基準とした点から他の点をマイナスするということですね。ちなみに(A-B)(A-C)の場合だと(B-A)(C-A)という風に基準点を後から引くパターンでも同じ計算結果が出ます。
どちらのやり方でも答えは同じなので、自分に合うやり方でやってみてください。
(補足)求積表の練習は必要?
土地家屋調査士試験の土地の図面では求積表を書く練習をしますね。
もちろん、求積表が全く書けないのはマズイですし、計算方法も一応は知っておいた方がいいです。
ですが、本試験に出題されるのはごく稀です。ほぼ作業みたいなもので、電卓の打ちミスさえしなければ誰でも書けますから。
求積表で地積の計算をするのはとても時間がかかるので、今回紹介した複素数計算で出した方がいいです。
とは言っても、絶対に出ないとは限らないので10回に1回くらいは求積表を書く練習をしておいた方がいいかもしれませんね。
さて、面積計算は複素数の理解が深まるため、次で紹介する交点計算へ進む準備が整います。これまでの流れとは少し変わるので複素数の計算に不安がある人はいったん戻って復習してください。
【応用編】交点計算の方法
交点計算は複素数ではなく、座標式を直接使う計算方法です。
複素数計算と併用されることが多いため、この章でまとめておきます。本試験で頻出のため、あえてここで説明しますが、まずは複素数をマスターして余力ができたらこの章に戻ってきてもいいです。
また、最初は実際の問題とこのページを見ながらゆっくりと操作になれてください。慣れれば必ずできるようになるので大丈夫です。では、行ってみましょう。

交点計算とは、直線と直線の交点の座標(未知点)を求めることです。
上の画像で言うと既知点(すでに座標が分かっている点)を結んだ線によって交点ができていますね。
赤い線と青い線が交わる部分のことです。この交点の座標を求める計算をこれからやっていきます。
注意点
F-789SGの仕様上、通常計算で使用する「CPLXモード」を交点計算で使用する「STATモード」に変換してしまうと、「CPLXモード」で予め記録したメモリーのY座標が消えます。
なので、通常計算用の関数電卓と交点計算用の関数電卓は分けたほうがいいです。同一機種でもいいので、1台しか持っていない人はもう1台買っておきましょう。
(※Y座標が削除される現象の回避策があるかもしれませんが、私自身は専門家ではありませんので詳細はメーカーに直接お問い合わせしてください)
交点計算をする前の設定
メモリーのリセット
まずは関数電卓の中に残っているメモリーをリセットしておきます。

分数表示からライン表示へ変更
続いて、分数表示をライン表示(小数点)に変更します。

(パターン①)通常の交点計算
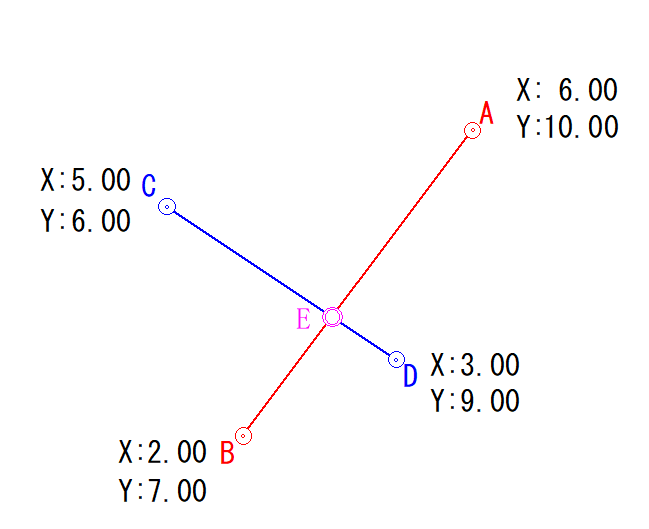
既知点ABCDがあり、直線ABと直線CDの交点がEです。
直線ABと直線CDの式をそれぞれ出して、その後に交点Eを求めます。
ところで、直線の式の公式を覚えていますか?中学校の数学で習います。
y=ax+b
aが傾き、bが切片(せっぺん)です。
これが通常の形なのですが、調査士試験の場合はちょっと違います。
Bが傾き、Aが切片です。関数電卓の仕様上、こちらの形を使うので気を付けて下さい。
計算の流れはこんな感じ。
- STATモードで直線AB、直線CDの傾きと切片を出す(それぞれメモリーする)
- EQNモードで直線AB、直線CDの交点を出す
STATモードで直線AB、直線CDの傾きと切片を出す
直線の式はSTATモードで出すことができます。※[MODE]は一番上の段、右から二番目にあります。
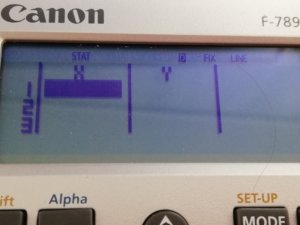
このような画面に切り替わると思います。これがSTATモードです。
まずは、直線ABを出します。それぞれの座標を打ち込んでいきます。
| X | Y | |
| A | 6 | 10 |
| B | 2 | 7 |
電卓のボタンの配置はこちら。

数字を打ち込んだら[=]を押すと確定できます。
[=]を押すと右の行ではなく、下の段に移動するので矢印ボタンで打ち込みたい場所までカーソルを移動させてください。
このような状態になればOKです。

慣れてくるとまずはX座標を全部打ち込んでからY座標を打ち込む・・・というテクニックも使えるようになりますが、ミスりやすいので気を付けて下さい。
あと、もしも打ち間違えたら、ミスしたところにカーソルを合わせて[DEL]キーを押せば消えます。
[CA]を押すと初期画面に戻るので注意。
先ほどの画面のままの人はいったん、[CA]を押して初期画面に戻ります。
続いて、傾きと切片を出します。
まずはA(切片)から出して、それをメモリーします。


[=]より前の操作で切片を出しています。[=]を押すと5.50と出るはずです。
[=]より後の操作で出した切片の値を[A]に記録しています。
続いてB(傾き)を出します。
先ほどとほとんど同じです。[=]を押すと0.75と出るはずです。
今度は[B]に記録させます。
傾きと切片をそれぞれ計算して関数電卓にメモリーしたってことですね。
ここまでで直線ABの式が出せました。
さて、次は直線CDを出します。
まずはSTATモードを起動します。やり方はさっきと同じ。今度は切片をC、傾きをDに記憶させましょう。
このような画面に切り替われば成功です。

続いて、CとDの座標を打ち込みます。
| X | Y | |
| C | 5 | 6 |
| D | 3 | 9 |
[CA]を押して初期画面に戻ります。
次に傾きと切片を出します。やり方はさっきと同じですが、関数電卓の表示上ではA=切片、B=傾きになっています。
AとBのメモリーは直線ABの計算の時に使ったので、今回は傾きをD、切片をCに入れます。分かりにくいのでミスしないように注意です。

まずは切片から出して、それをCのボタンにメモリーします。(切片は13.50です)
続いて傾きを出して、Dにメモリーします。(傾きは-1.50になります)
EQNモードで交点の座標を出す
ここまでの計算で直線ABと直線CDの式が出せました。
下の画像だと赤い線と青い線の式を出したところです。
- 直線ABの式:-BX+Y=A
- 直線CDの式:-DX+Y=C
ここから交点E(ピンクの点)を出していきます。

交点を出す際に使うのは「EQN」モードです。さっそく起動してみます。
このような画面になりますね。

ここで、直線の公式を思い出します。
この形でしたね。今回計算した値を当てはめるとこんな感じ。
- 直線ABの式:-BX+Y=A
- 直線CDの式:-DX+Y=C
先ほど起動したEQNモードでは
aX + bY = c という形になっています。つまり
| a(X) | b(Y) | c | |
| 1 | -B | 1 | A |
| 2 | -D | 1 | C |
こうなりますね。(Yの前には一見すると何もありませんが数字の1が隠れています。※1×Yの1が省略された形です)
これらをそれぞれ打ち込んでいきます。(aの欄にはマイナスがつくことに注意)
これで一段目が入力されていますね。続いて二段目です。
二段目の入力が終わりました。画面はこのようになっています。

続けて、[=]を押すとX座標が表示されます。
X=3.56です。(32」9と表示される人は[F←→D]ボタンを押してください)
続けて、[=]を押すとY座標が表示されます。
Y=8.17です。
これで、直線ABと直線CDの交点であるEの座標が出ました。
答え:E(3.56 , 8.17)
これが基本の形です。最初は難しいですが何度も解けばすらすら解けるようになります。
(パターン②)直線の式との交点の場合
Xの座標値が同じパターン

ここからは応用編。このパターンもよく出ます。
直線ABは先ほどと同じ式です。
ここで直線DFに注目してください。
| X | Y | |
| D | 3 | 9 |
| F | 3 | 6 |
それぞれのXの値が同じですね。このようなパターンでは先ほどのようにSTATモードで直線DFの式を出すことができません。
ですが、直線DF上に交点Gがあるので、GのX座標も3だということが分かりますね。
G:X=3、Y=?
こんな感じ。Xの座標はすでに分かっているのであとはYを出すだけです。
ここで先ほどの直線ABの式が出てきます。
-BX+Y=A
変形すると
Y=A+BX
になります。(-BXを右側に移項。※移項すると符号が変わります(+は-、-は+になる))
ここで、AとBとXの値はすでに出ていますね。AとBの値はさっきSTATモードで出しています。
すでに関数電卓に記憶させているのでそのまま使えます。
A=切片、B=傾き、X=3です。
では、Yを出しましょう。
EQNモードのままになっている人は複素数モードに切り替えます。
次に、Y=A+BXの式に当てはめていきます。

7.75と出ればOKです。
答え:G(3, 7.75)
Yの座標値が同じパターン
先ほどはX座標が同じ場合のパターンを紹介しました。
| X | Y | |
| D | 3 | 9 |
| F | 3 | 6 |
↑この場合はYの座標が知りたいので-BX+Y=AをY=A+BXに変形しましたね。
逆にY座標が同じパターンでも使えます。
| X | Y | |
| D | 9 | 3 |
| F | 6 | 3 |
Yの座標が同じです。つまりY=3です。
この場合はX座標を求める必要があるので
-BX+Y=AをX=●●の形に変形します。こっちの変形はちょっとめんどくさいです。
できれば完成形を丸覚えしたほうがいいです。
- -BX+Y=A
- BX-Y=-A《すべての値に×(-1)をして符号を変えた》
- BX=Y-A《Yを移項した》
- X=(Y-A)÷B《両辺をBで割った。この式を丸覚えしよう》
この式に当てはめていきます。※[ ( ]と[ ) ]は数字の9の上あたりにあります。
※[-]は[=]の隣にある普通の引き算です。[(−)]ではないので注意。

-3.33と出れば正解です。
答え:(-3.33 , 3)
注意点ですが、今回紹介した方法はF-789SG(キャノン)で交点計算をするやり方です。
カシオを使う場合はやり方が違うので気を付けてください。
まとめ:操作を覚えたら「記述式」の問題で定着させよう
今回解説した「複素数モード」や「メモリー機能」は、土地家屋調査士試験に合格するための最強の武器です。
しかし、操作方法を知っているだけでは意味がありません。実際に問題を解いて、指が勝手に動くレベルまで落とし込む必要があります。
関数電卓の使い方をマスターしたあなたが次にやるべきことは、「記述式(土地)」の問題演習です。
ここを徹底的に反復することで、計算スピードは飛躍的に向上します。
「電卓の使い方はわかったけど、実際にどの問題集をどう解けばいいの?」
そんな疑問を持つあなたへ、独学でも記述式を得点源にするための具体的な勉強法をまとめました。
関数電卓をフル活用して、記述式の基準点を確実に突破するテクニックを確認しましょう。

