

二点間距離って関数電卓で出せるの?やり方を教えてほしい!
そんな疑問にお答えします。
今回は二点間距離(=筆界点間の距離)の求め方です。
複素数モードが使える段階まで進んでいることを前提として話を進めていきますので、まだ設定が終わっていない人は下の記事を読んでくださいね。
使う機種はキF-789SG(キャノン)です。

座標を記憶させる
計算を始める前に前回使ったT1、T2の座標を[A]と[B]に記憶させておいてください。
| X | Y | |
| T1 | 100 | 100 |
| T2 | -150 | 200 |
関数電卓[F-789SG]で点間距離を求める方法

では、上のT1とT2の距離を求めてみましょう!上の図でピンク色の線の部分です。 距離は[Abs]を使い求めることができます。

答えはフル桁だと269.2582404となります。
小数点以下第3位を四捨五入した数値は269.26となります。四捨五入の方法はこちらに書いています。
参考:【土地家屋調査士】関数電卓[F-789SG]の使い方|設定をリセット、メモリー方法、ライン表示、丸め、複素数モードに変更
ちなみに計算した辺長を次の計算で使う場合は、フル桁のまま使っても、四捨五入した値を使っても答えに大差はないです。
こちらで詳しく解説している先生がいるので参考にしてください。
参考:早くて正確に!複素数による測量計算ミニ講座③特殊な関数
できましたか? ※ [Alpha]を[RCT]に置き換えても計算できます。少し練習してみましょう。
練習問題
| A | 100 | 100 |
| B | 150 | 300 |
| C | 300 | 250 |
| D | 200 | 50 |
まずはこの座標を電卓に入力してください。一度メモリーをクリアにするか、先ほどのT1、T2に上書きする形で大丈夫です。
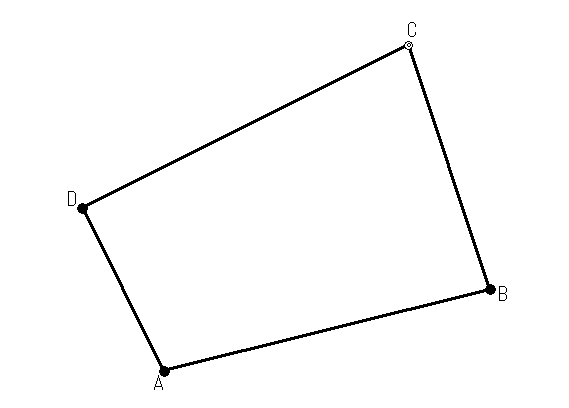
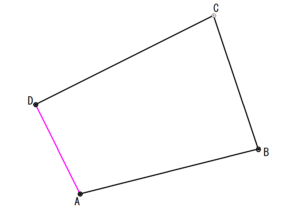
こんな感じの配置です。ではそれぞれの距離を計算してみます。
A→Bの距離
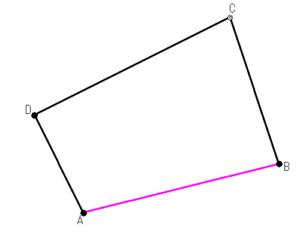
B→Cの距離
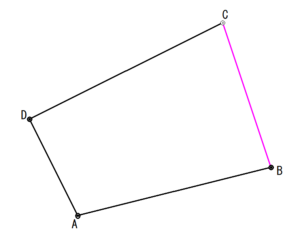
C→Dの距離
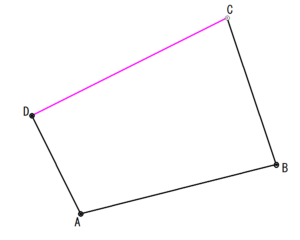
A→Dの距離
三平方の定理を使った計算方法
先ほどの計算方法は複素数を使ったものですが、三平方の定理を利用して答えを出すこともできます。
複素数を利用した方が早いのですが、テキストの解答にはこちらの方法が載っていることがあるので一応ご紹介しておきます。
例としてA→B間の距離を出してみます。
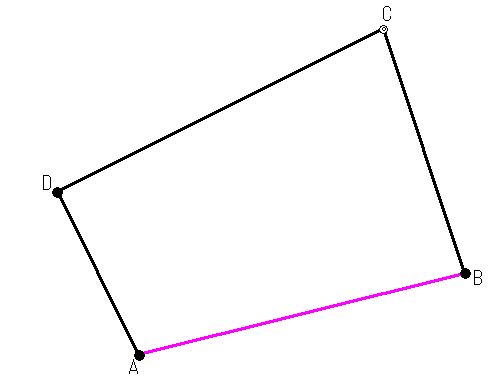
答えは206.1552813mでしたね。解き方を出す前に三平方の定理を復習しておきます。
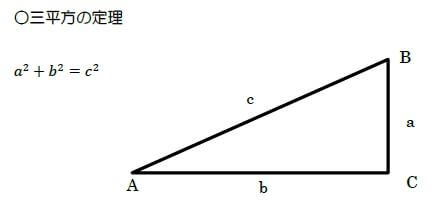
出したい部分は「c」の辺長つまり斜辺ですね。
この式を変形します。
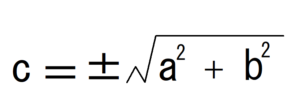
辺長は「正の数」なので「+」を採用します。答えが「−100m」なんておかしいですからね。さて、この式にAとBの座標を当てはめてみます。
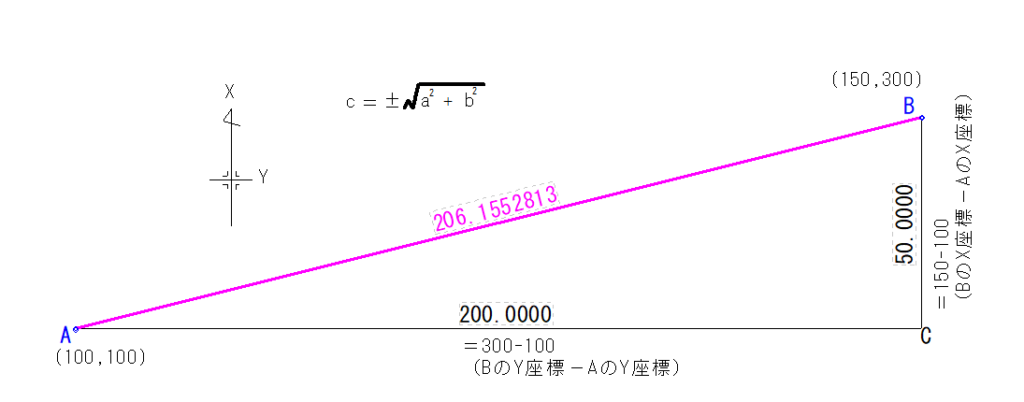
図の通り、X座標同士、Y座標同士を引いてそれを二乗しています。A-BでもB-Aでもいいです。どうせ二乗するので答えは同じです。(マイナス×マイナスはプラスになりますからね)


打ち方としてはこのようになります。この解き方は複素数を知っているならばそんなに重要ではないです。ですが、東京法経学院などのテキストを見ると解説の解き方はこちらになっていることが多いんですよね。
なので一応知っておくと良いです。筆界点間の距離の出し方は以上です。何度も挑戦してマスターしてくださいね。
では、今回の記事はここまでです。
他の計算方法についてはこちらに書いています。
参考:【土地家屋調査士】複素数を使って最短で試験に合格する方法|F-789SG-SL(キャノン)




