
【こんな不安はありませんか】
- 数学が苦手だけど測量士補・土地家屋調査士の計算はできるか
- 具体的にどこから手を付けていいのか分からない
そんな不安に答えるために、試験で本当に使う公式だけをまとめました。
土地家屋調査士・測量士補の計算は、難しい数学というより「どの場面で、どの公式を使うか」の型がほとんどです。
まずはこのページをブックマークして、問題を解きながら「辞書」みたいに使ってください。
- 三平方の定理(直角三角形の距離)
- 正弦定理(角・辺の関係)
- 余弦定理(2辺と角/3辺の関係)
- 内分点・外分点(座標の「割り算」)
- 二辺夾角の面積(面積を最短で出す)
※公式の暗記より「使いどころ」を覚える方が100倍大事です。
図形の公式の前に:最低限おさえる2つ(平方根・三角比)
図形の公式そのものよりも、つまずきやすいのがこの2つです。
- 平方根(√):ルートの計算・近似(小数にする)
- 三角比(sin / cos / tan):角度と辺の関係
ここが不安な人は、まず下の解説を一度だけ見ておくと早いです(試験用に深くやる必要はありません)。
- 平方根の確認:平方根の基本
- 三角比の確認(動画が分かりやすい):sin・cos・tanの基本
三平方の定理(直角三角形の距離)
直角三角形の斜辺の二乗は、底辺の二乗+高さの二乗。
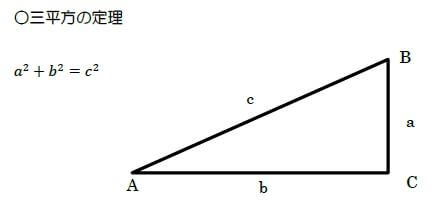
【どんなときに使う?】
- 2点間の距離を出したい(直角が作れる/直角に分解できる)
- 座標・作図で「斜めの距離」を最短で出したい
【ミス防止ポイント】
- 直角がある(作れる)かをまず確認
- 最後は√を忘れない(2乗のまま終わらない)
正弦定理(角・辺の関係)
角度や距離を出したいときに使います。余弦定理より計算がシンプルな場面が多いので、使えるなら正弦定理が安全です。
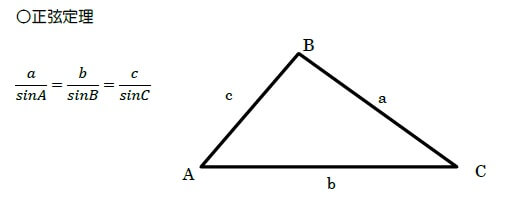
【どんなときに使う?】
- 三角形で「角が1つ分かって、辺も一部わかる」→残りを出す
- 測量士補で出る“角と距離”系の基本処理
参考(図で確認したい人向け):正弦定理の確認
余弦定理(2辺と角/3辺の関係)
式が少し複雑ですが、慣れると「これしかない」場面が多いです。正弦定理が使えないときの本命。
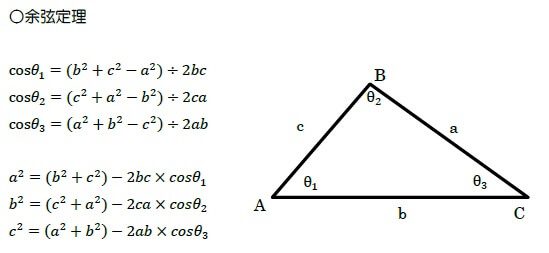
【どんなときに使う?】
- 2辺とその間の角(夹角)が分かる → 残りの辺を出す
- 3辺のうち2辺+角度から距離を出す必要がある
【ミス防止ポイント】
- 符号(−2ab cosC)を間違えやすいので、式は毎回そのまま書く
- cosを使う角は「2辺の間の角」
参考:余弦定理の確認
内分点・外分点(座標の「割り算」)
土地家屋調査士の記述式(特に土地)で非常によく出ます。第1問目の定番になりやすい論点です。
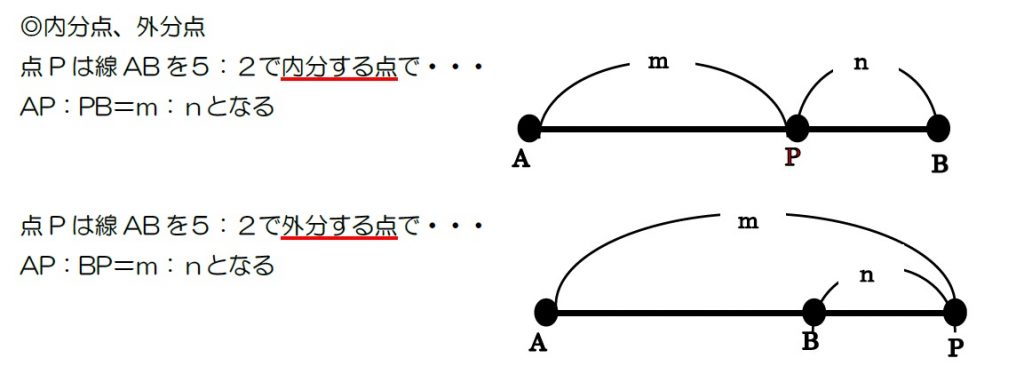
【どんなときに使う?】
- 点A〜点Bを「m:n」で割った点の座標を出す
- 境界点が“等分/比”で与えられる問題(実務でも出る考え方)
【ミス防止ポイント】
- 比(m:n)をひっくり返さない(A側がmか、B側がmか)
- 座標はxとyを同じ手順で計算する(片方だけ式を変えない)
「まず概念を動画で掴みたい」人向け:内分点と外分点(概念)
※試験は座標で計算します。座標の例も見たい人向け:内分点(座標寄りの解説)
二辺夾角による面積計算(最短で面積を出す)
二辺とその間の角が分かるなら、面積はこの公式が最速です。覚えておくと記述式で時間短縮になります。
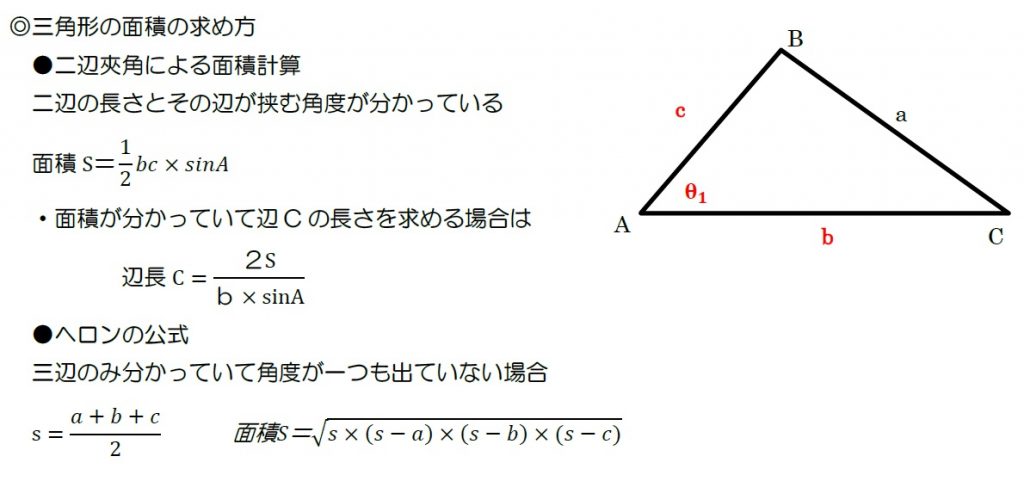
【どんなときに使う?】
- 三角形の面積を、底辺×高さを作らずに出せる
- 土地の面積計算で「高さを作ると遠回り」なとき
覚え方のコツ:公式は「暗記」より「反射」にする
公式を眺めるだけだと、試験本番で出てきません。おすすめはこの順番です。
- このページの画像(公式一覧)を見ながら、問題を1問解く
- 解けなかったら、どの公式を使う場面だったかだけチェック
- 同じタイプを2〜3問やって「反射」で出るようにする
「数学ができる人」より「同じ型を繰り返した人」が勝ちます。
次にやるべきこと
公式を確認したら、次は「何を、どの順番でやるか」です。
参考:測量士補を独学1ヶ月で一発合格|土地家屋調査士 午前免除を最短で取る方法
今回の記事はここまでです。

